Tensor-based framework for training flexible neural networks
Paper and Code
Jun 25, 2021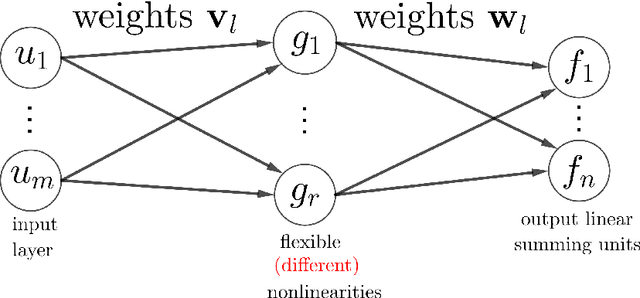
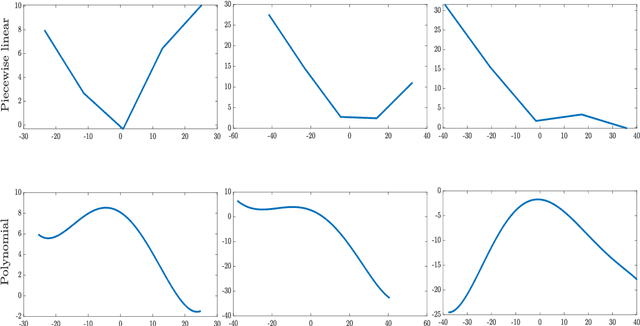
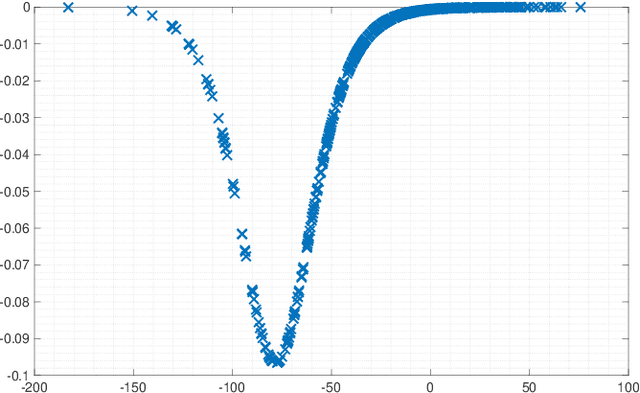
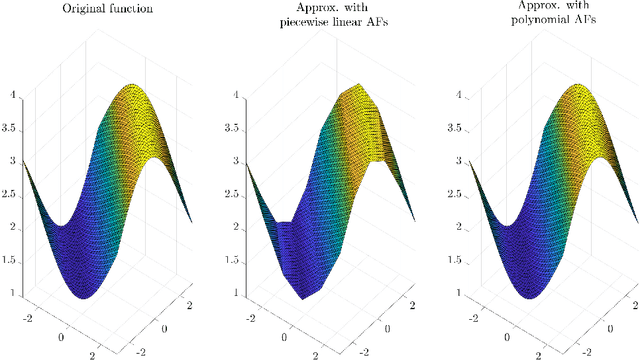
Activation functions (AFs) are an important part of the design of neural networks (NNs), and their choice plays a predominant role in the performance of a NN. In this work, we are particularly interested in the estimation of flexible activation functions using tensor-based solutions, where the AFs are expressed as a weighted sum of predefined basis functions. To do so, we propose a new learning algorithm which solves a constrained coupled matrix-tensor factorization (CMTF) problem. This technique fuses the first and zeroth order information of the NN, where the first-order information is contained in a Jacobian tensor, following a constrained canonical polyadic decomposition (CPD). The proposed algorithm can handle different decomposition bases. The goal of this method is to compress large pretrained NN models, by replacing subnetworks, {\em i.e.,} one or multiple layers of the original network, by a new flexible layer. The approach is applied to a pretrained convolutional neural network (CNN) used for character classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge