Polarimetric phase retrieval: uniqueness and algorithms
Paper and Code
Jun 26, 2022
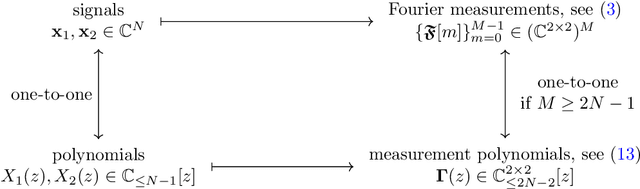

This work introduces a novel Fourier phase retrieval model, called polarimetric phase retrieval that enables a systematic use of polarization information in Fourier phase retrieval problems. We provide a complete characterization of uniqueness properties of this new model by unraveling equivalencies with a peculiar polynomial factorization problem. We introduce two different but complementary categories of reconstruction methods. The first one is algebraic and relies on the use of approximate greatest common divisor computations using Sylvester matrices. The second one carefully adapts existing algorithms for Fourier phase retrieval, namely semidefinite positive relaxation and Wirtinger-Flow, to solve the polarimetric phase retrieval problem. Finally, a set of numerical experiments permits a detailed assessment of the numerical behavior and relative performances of each proposed reconstruction strategy. We further highlight a reconstruction strategy that combines both approaches for scalable, computationally efficient and asymptotically MSE optimal performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge