Structure of Artificial Neural Networks -- Empirical Investigations

Within one decade, Deep Learning overtook the dominating solution methods of countless problems of artificial intelligence. ``Deep'' refers to the deep architectures with operations in manifolds of which there are no immediate observations. For these deep architectures some kind of structure is pre-defined -- but what is this structure? With a formal definition for structures of neural networks, neural architecture search problems and solution methods can be formulated under a common framework. Both practical and theoretical questions arise from closing the gap between applied neural architecture search and learning theory. Does structure make a difference or can it be chosen arbitrarily? This work is concerned with deep structures of artificial neural networks and examines automatic construction methods under empirical principles to shed light on to the so called ``black-box models''. Our contributions include a formulation of graph-induced neural networks that is used to pose optimisation problems for neural architecture. We analyse structural properties for different neural network objectives such as correctness, robustness or energy consumption and discuss how structure affects them. Selected automation methods for neural architecture optimisation problems are discussed and empirically analysed. With the insights gained from formalising graph-induced neural networks, analysing structural properties and comparing the applicability of neural architecture search methods qualitatively and quantitatively we advance these methods in two ways. First, new predictive models are presented for replacing computationally expensive evaluation schemes, and second, new generative models for informed sampling during neural architecture search are analysed and discussed.

Efficient NAS with FaDE on Hierarchical Spaces

Neural architecture search (NAS) is a challenging problem. Hierarchical search spaces allow for cheap evaluations of neural network sub modules to serve as surrogate for architecture evaluations. Yet, sometimes the hierarchy is too restrictive or the surrogate fails to generalize. We present FaDE which uses differentiable architecture search to obtain relative performance predictions on finite regions of a hierarchical NAS space. The relative nature of these ranks calls for a memory-less, batch-wise outer search algorithm for which we use an evolutionary algorithm with pseudo-gradient descent. FaDE is especially suited on deep hierarchical, respectively multi-cell search spaces, which it can explore by linear instead of exponential cost and therefore eliminates the need for a proxy search space. Our experiments show that firstly, FaDE-ranks on finite regions of the search space correlate with corresponding architecture performances and secondly, the ranks can empower a pseudo-gradient evolutionary search on the complete neural architecture search space.

GRAN is superior to GraphRNN: node orderings, kernel- and graph embeddings-based metrics for graph generators

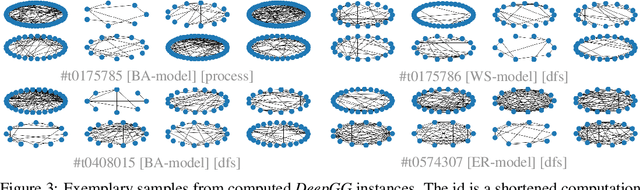
A wide variety of generative models for graphs have been proposed. They are used in drug discovery, road networks, neural architecture search, and program synthesis. Generating graphs has theoretical challenges, such as isomorphic representations -- evaluating how well a generative model performs is difficult. Which model to choose depending on the application domain? We extensively study kernel-based metrics on distributions of graph invariants and manifold-based and kernel-based metrics in graph embedding space. Manifold-based metrics outperform kernel-based metrics in embedding space. We use these metrics to compare GraphRNN and GRAN, two well-known generative models for graphs, and unveil the influence of node orderings. It shows the superiority of GRAN over GraphRNN - further, our proposed adaptation of GraphRNN with a depth-first search ordering is effective for small-sized graphs. A guideline on good practices regarding dataset selection and node feature initialization is provided. Our work is accompanied by open-source code and reproducible experiments.

deepstruct -- linking deep learning and graph theory

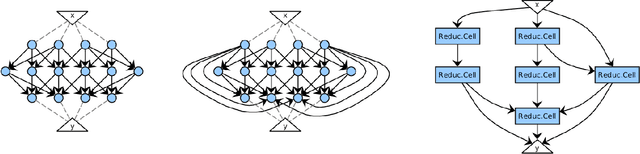
deepstruct connects deep learning models and graph theory such that different graph structures can be imposed on neural networks or graph structures can be extracted from trained neural network models. For this, deepstruct provides deep neural network models with different restrictions which can be created based on an initial graph. Further, tools to extract graph structures from trained models are available. This step of extracting graphs can be computationally expensive even for models of just a few dozen thousand parameters and poses a challenging problem. deepstruct supports research in pruning, neural architecture search, automated network design and structure analysis of neural networks.

Experiments on Properties of Hidden Structures of Sparse Neural Networks

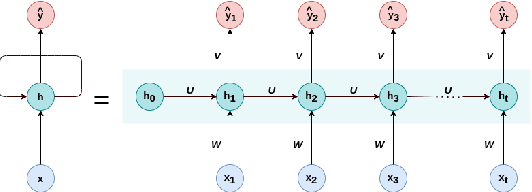
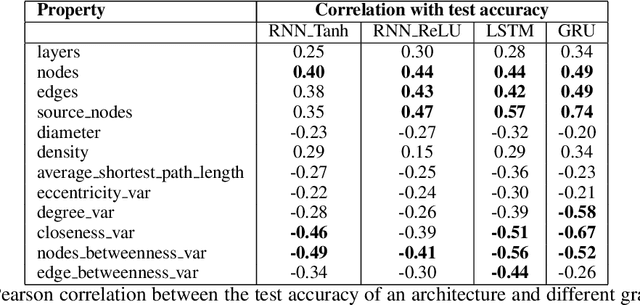
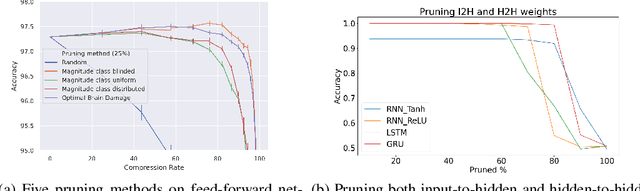
Sparsity in the structure of Neural Networks can lead to less energy consumption, less memory usage, faster computation times on convenient hardware, and automated machine learning. If sparsity gives rise to certain kinds of structure, it can explain automatically obtained features during learning. We provide insights into experiments in which we show how sparsity can be achieved through prior initialization, pruning, and during learning, and answer questions on the relationship between the structure of Neural Networks and their performance. This includes the first work of inducing priors from network theory into Recurrent Neural Networks and an architectural performance prediction during a Neural Architecture Search. Within our experiments, we show how magnitude class blinded pruning achieves 97.5% on MNIST with 80% compression and re-training, which is 0.5 points more than without compression, that magnitude class uniform pruning is significantly inferior to it and how a genetic search enhanced with performance prediction achieves 82.4% on CIFAR10. Further, performance prediction for Recurrent Networks learning the Reber grammar shows an $R^2$ of up to 0.81 given only structural information.

Deep Graph Generators

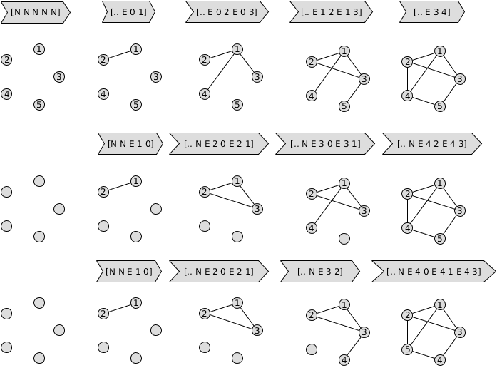
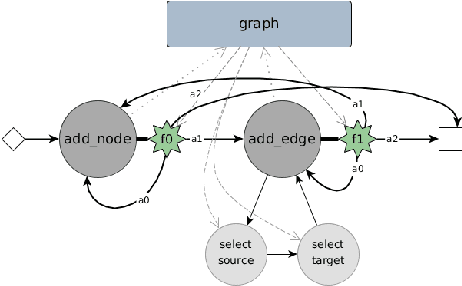
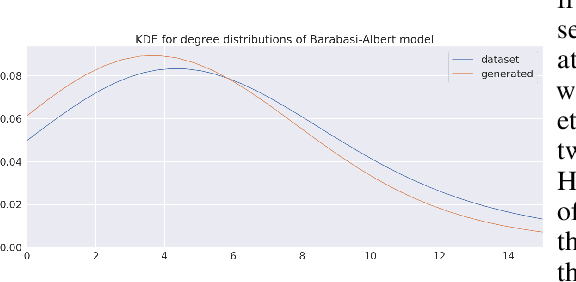
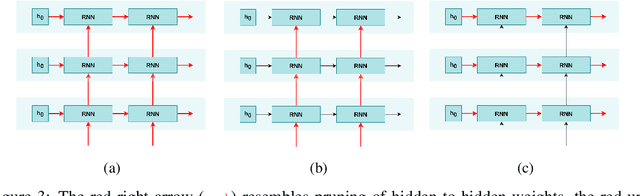
Learning distributions of graphs can be used for automatic drug discovery, molecular design, complex network analysis and much more. We present an improved framework for learning generative models of graphs based on the idea of deep state machines. To learn state transition decisions we use a set of graph and node embedding techniques as memory of the state machine. Our analysis is based on learning the distribution of random graph generators for which we provide statistical tests to determine which properties can be learned and how well the original distribution of graphs is represented. We show that the design of the state machine favors specific distributions. Models of graphs of size up to 150 vertices are learned. Code and parameters are publicly available to reproduce our results.

Structural Analysis of Sparse Neural Networks

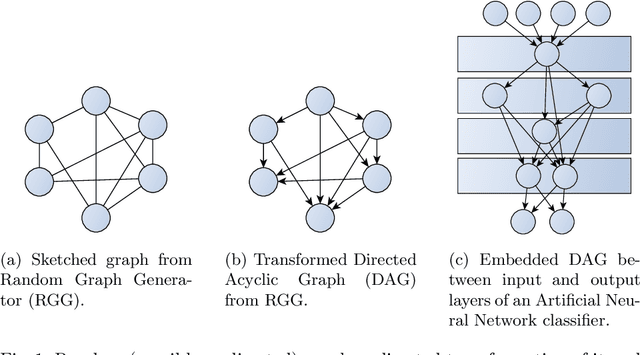
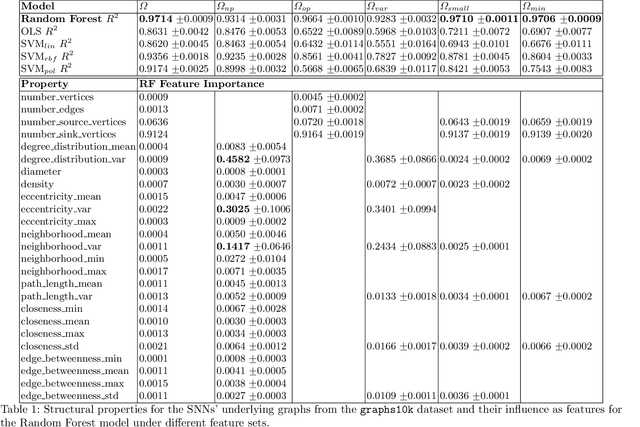
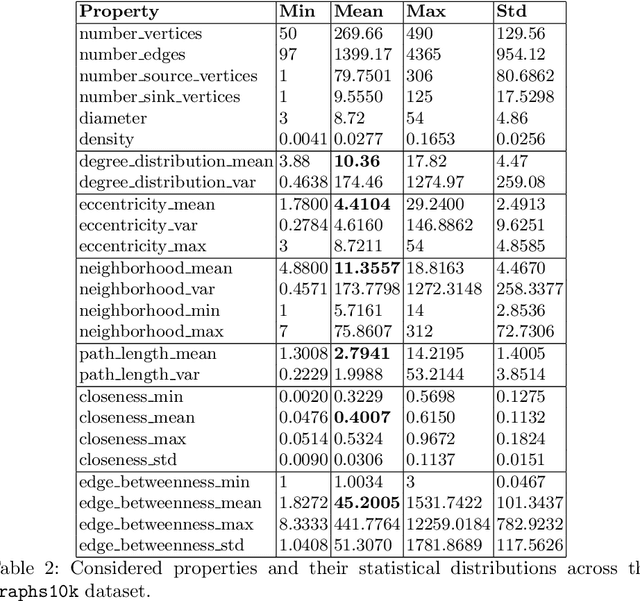
Sparse Neural Networks regained attention due to their potential for mathematical and computational advantages. We give motivation to study Artificial Neural Networks (ANNs) from a network science perspective, provide a technique to embed arbitrary Directed Acyclic Graphs into ANNs and report study results on predicting the performance of image classifiers based on the structural properties of the networks' underlying graph. Results could further progress neuroevolution and add explanations for the success of distinct architectures from a structural perspective.

Analysing Neural Network Topologies: a Game Theoretic Approach

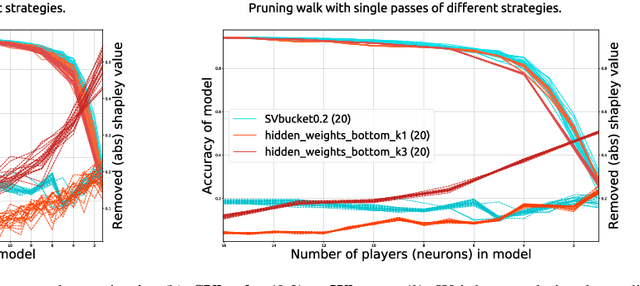
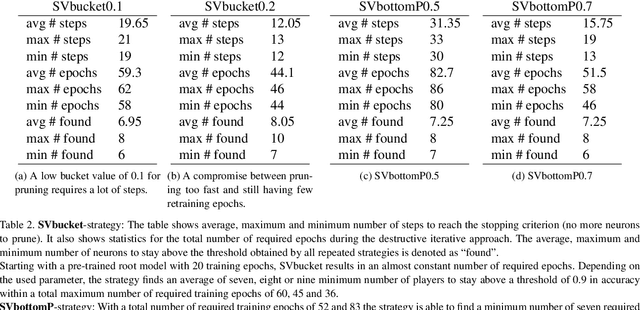
Artificial Neural Networks have shown impressive success in very different application cases. Choosing a proper network architecture is a critical decision for a network's success, usually done in a manual manner. As a straightforward strategy, large, mostly fully connected architectures are selected, thereby relying on a good optimization strategy to find proper weights while at the same time avoiding overfitting. However, large parts of the final network are redundant. In the best case, large parts of the network become simply irrelevant for later inferencing. In the worst case, highly parameterized architectures hinder proper optimization and allow the easy creation of adverserial examples fooling the network. A first step in removing irrelevant architectural parts lies in identifying those parts, which requires measuring the contribution of individual components such as neurons. In previous work, heuristics based on using the weight distribution of a neuron as contribution measure have shown some success, but do not provide a proper theoretical understanding. Therefore, in our work we investigate game theoretic measures, namely the Shapley value (SV), in order to separate relevant from irrelevant parts of an artificial neural network. We begin by designing a coalitional game for an artificial neural network, where neurons form coalitions and the average contributions of neurons to coalitions yield to the Shapley value. In order to measure how well the Shapley value measures the contribution of individual neurons, we remove low-contributing neurons and measure its impact on the network performance. In our experiments we show that the Shapley value outperforms other heuristics for measuring the contribution of neurons.