Well-posedness of a nonlinear integro-differential problem and its rearranged formulation

We study the existence and uniqueness of solutions of a nonlinear integro-differential problem which we reformulate introducing the notion of the decreasing rearrangement of the solution. A dimensional reduction of the problem is obtained and a detailed analysis of the properties of the solutions of the model is provided. Finally, a fast numerical method is devised and implemented to show the performance of the model when typical image processing tasks such as filtering and segmentation are performed.

On a fast bilateral filtering formulation using functional rearrangements

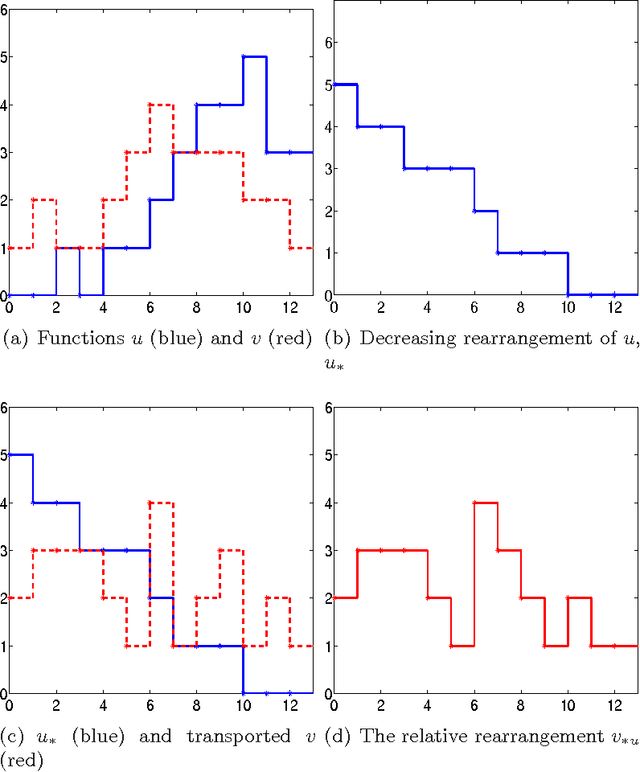
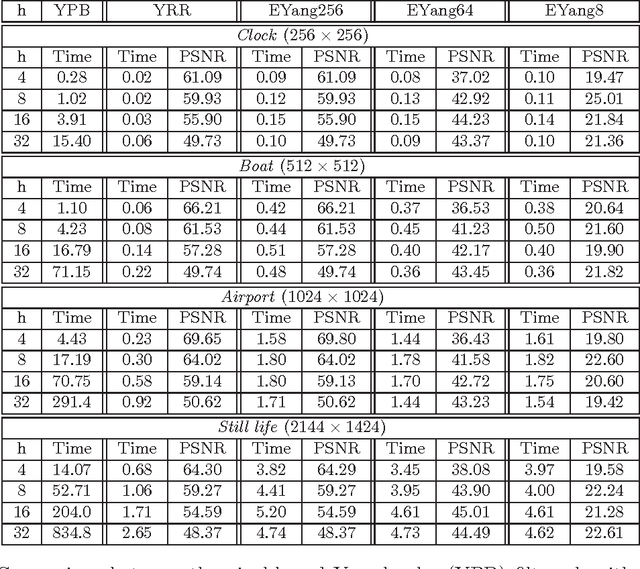
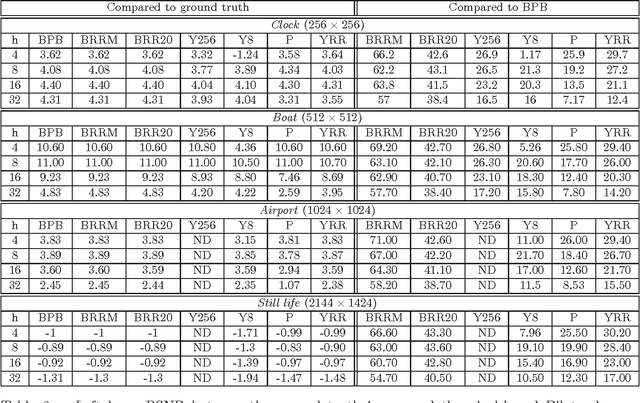
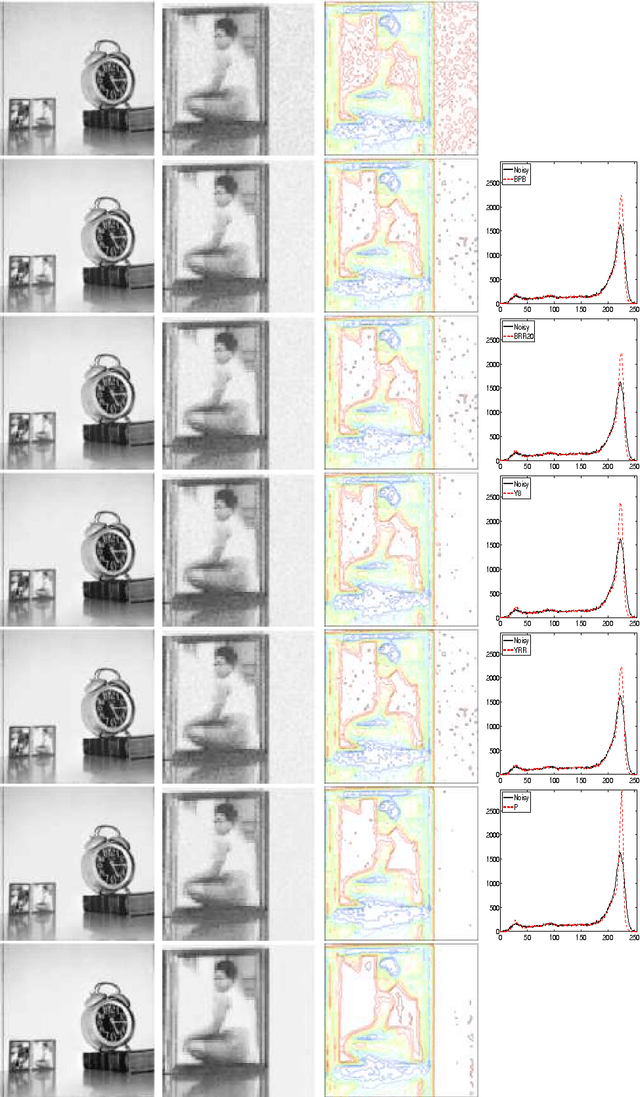
We introduce an exact reformulation of a broad class of neighborhood filters, among which the bilateral filters, in terms of two functional rearrangements: the decreasing and the relative rearrangements. Independently of the image spatial dimension (one-dimensional signal, image, volume of images, etc.), we reformulate these filters as integral operators defined in a one-dimensional space corresponding to the level sets measures. We prove the equivalence between the usual pixel-based version and the rearranged version of the filter. When restricted to the discrete setting, our reformulation of bilateral filters extends previous results for the so-called fast bilateral filtering. We, in addition, prove that the solution of the discrete setting, understood as constant-wise interpolators, converges to the solution of the continuous setting. Finally, we numerically illustrate computational aspects concerning quality approximation and execution time provided by the rearranged formulation.

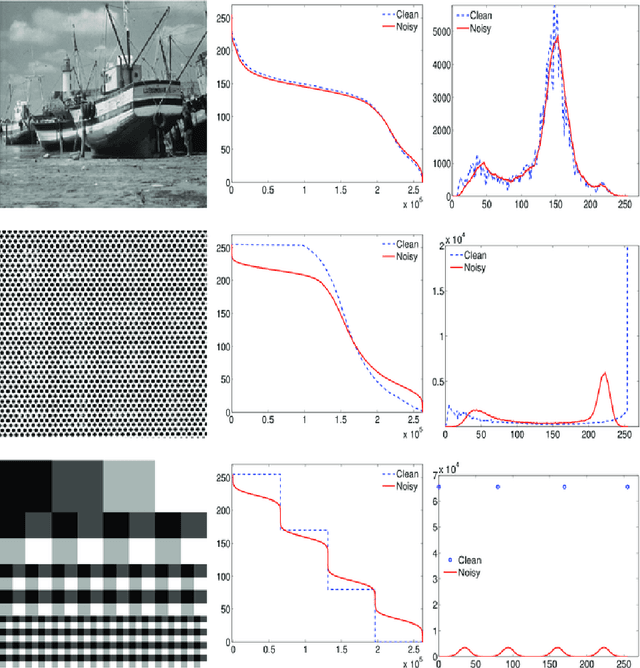
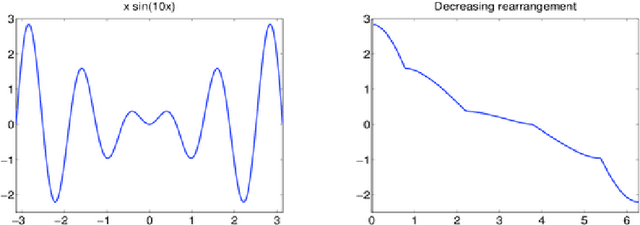
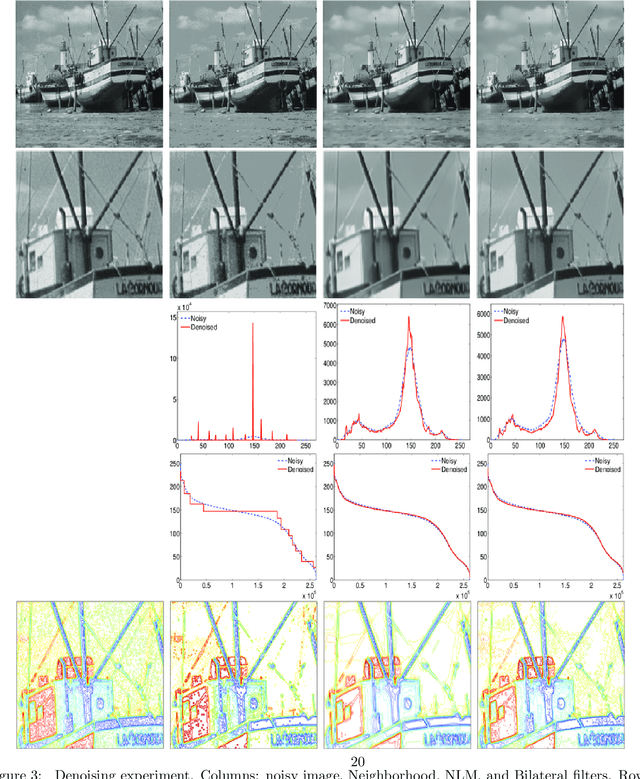
Neighborhood filters and the decreasing rearrangement

Nonlocal filters are simple and powerful techniques for image denoising. In this paper, we give new insights into the analysis of one kind of them, the Neighborhood filter, by using a classical although not very common transformation: the decreasing rearrangement of a function (the image). Independently of the dimension of the image, we reformulate the Neighborhood filter and its iterative variants as an integral operator defined in a one-dimensional space. The simplicity of this formulation allows to perform a detailed analysis of its properties. Among others, we prove that the filter behaves asymptotically as a shock filter combined with a border diffusive term, responsible for the staircaising effect and the loss of contrast.

On a new formulation of nonlocal image filters involving the relative rearrangement

Nonlocal filters are simple and powerful techniques for image denoising. In this paper we study the reformulation of a broad class of nonlocal filters in terms of two functional rearrangements: the decreasing and the relative rearrangements. Independently of the dimension of the image, we reformulate these filters as integral operators defined in a one-dimensional space corresponding to the level sets measures. We prove the equivalency between the original and the rearranged versions of the filters and propose a discretization in terms of constant-wise interpolators, which we prove to be convergent to the solution of the continuous setting. For some particular cases, this new formulation allows us to perform a detailed analysis of the filtering properties. Among others, we prove that the filtered image is a contrast change of the original image, and that the filtering procedure behaves asymptotically as a shock filter combined with a border diffusive term, responsible for the staircaising effect and the loss of contrast.

On a non-local spectrogram for denoising one-dimensional signals

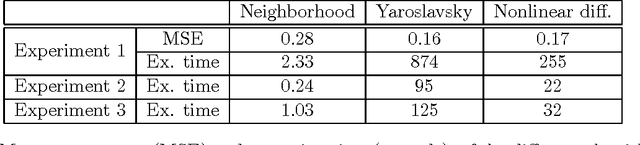
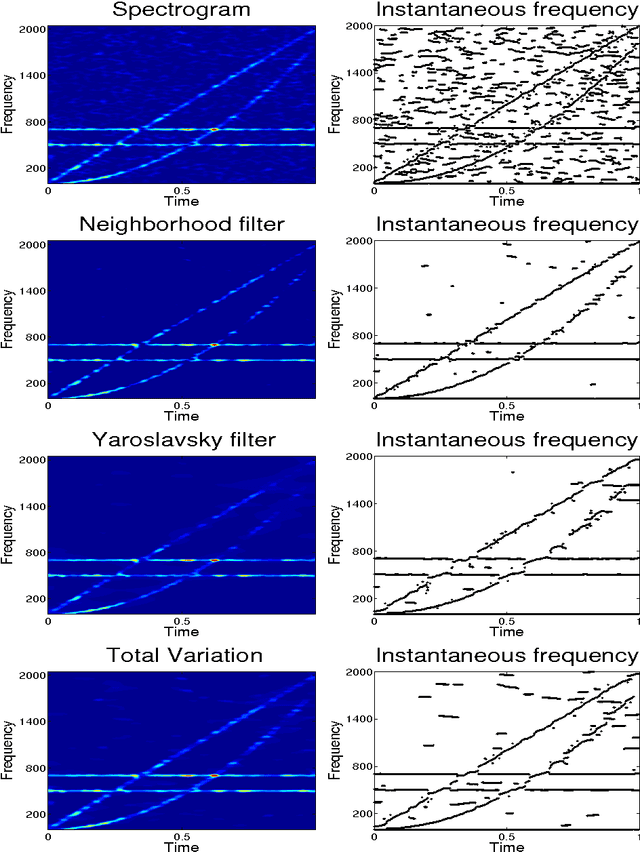
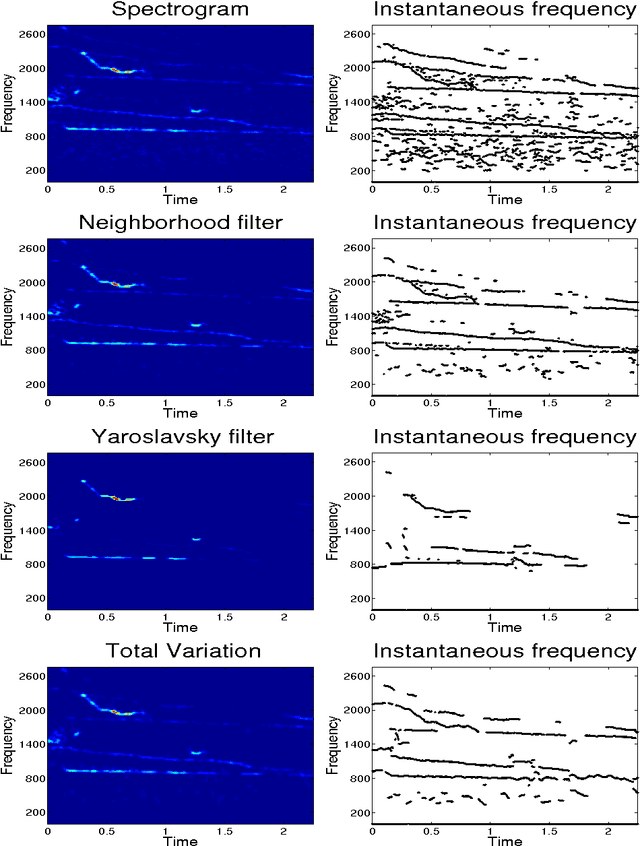
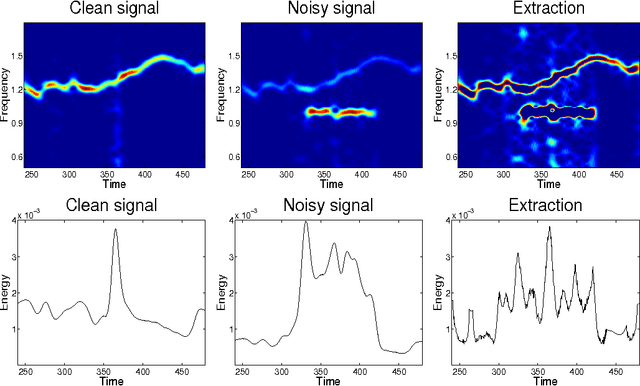
In previous works, we investigated the use of local filters based on partial differential equations (PDE) to denoise one-dimensional signals through the image processing of time-frequency representations, such as the spectrogram. In this image denoising algorithms, the particularity of the image was hardly taken into account. We turn, in this paper, to study the performance of non-local filters, like Neighborhood or Yaroslavsky filters, in the same problem. We show that, for certain iterative schemes involving the Neighborhood filter, the computational time is drastically reduced with respect to Yaroslavsky or nonlinear PDE based filters, while the outputs of the filtering processes are similar. This is heuristically justified by the connection between the (fast) Neighborhood filter applied to a spectrogram and the corresponding Nonlocal Means filter (accurate) applied to the Wigner-Ville distribution of the signal. This correspondence holds only for time-frequency representations of one-dimensional signals, not to usual images, and in this sense the particularity of the image is exploited. We compare though a series of experiments on synthetic and biomedical signals the performance of local and non-local filters.