On a fast bilateral filtering formulation using functional rearrangements
Paper and Code
May 03, 2015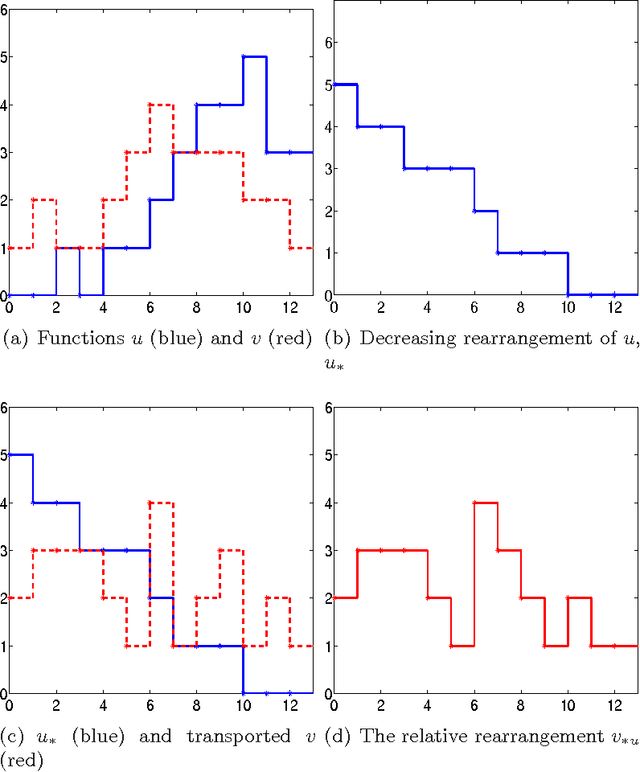
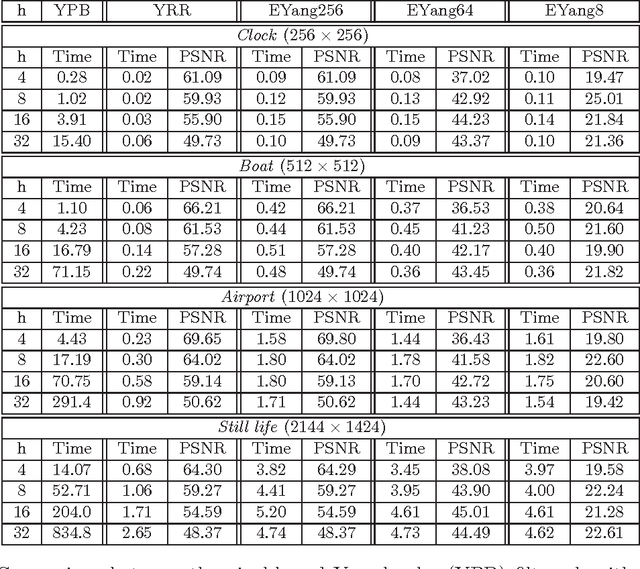
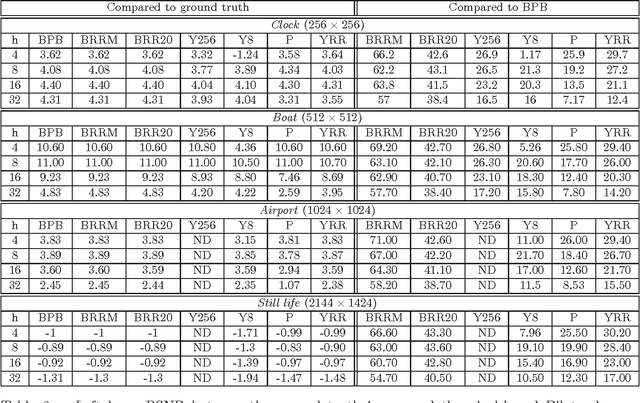
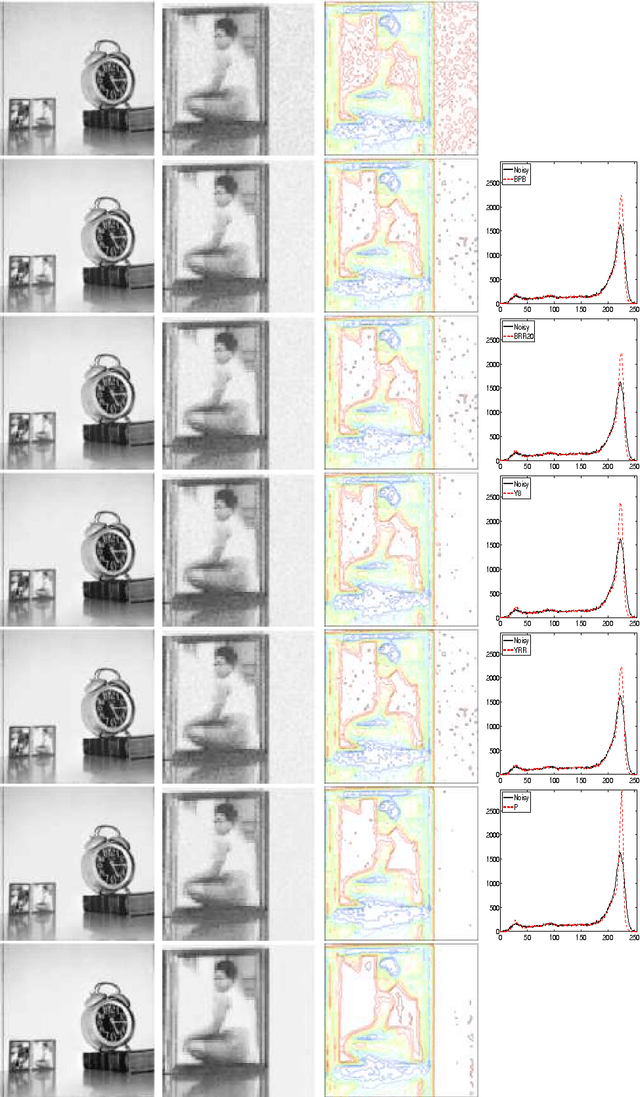
We introduce an exact reformulation of a broad class of neighborhood filters, among which the bilateral filters, in terms of two functional rearrangements: the decreasing and the relative rearrangements. Independently of the image spatial dimension (one-dimensional signal, image, volume of images, etc.), we reformulate these filters as integral operators defined in a one-dimensional space corresponding to the level sets measures. We prove the equivalence between the usual pixel-based version and the rearranged version of the filter. When restricted to the discrete setting, our reformulation of bilateral filters extends previous results for the so-called fast bilateral filtering. We, in addition, prove that the solution of the discrete setting, understood as constant-wise interpolators, converges to the solution of the continuous setting. Finally, we numerically illustrate computational aspects concerning quality approximation and execution time provided by the rearranged formulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge