Neighborhood filters and the decreasing rearrangement
Paper and Code
Jun 27, 2014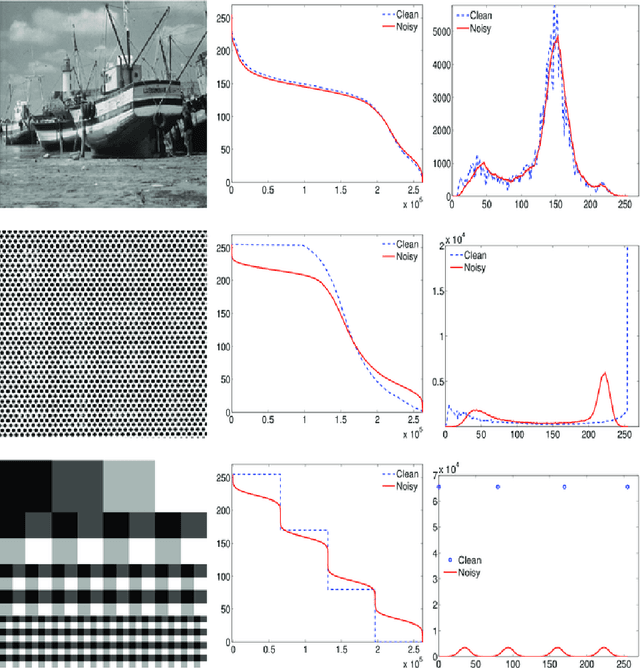
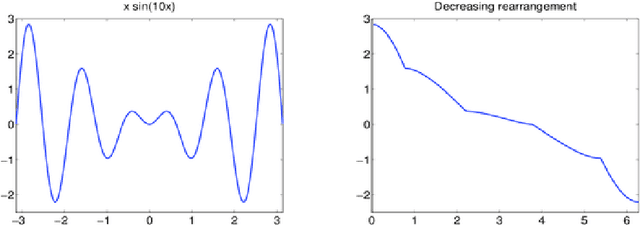
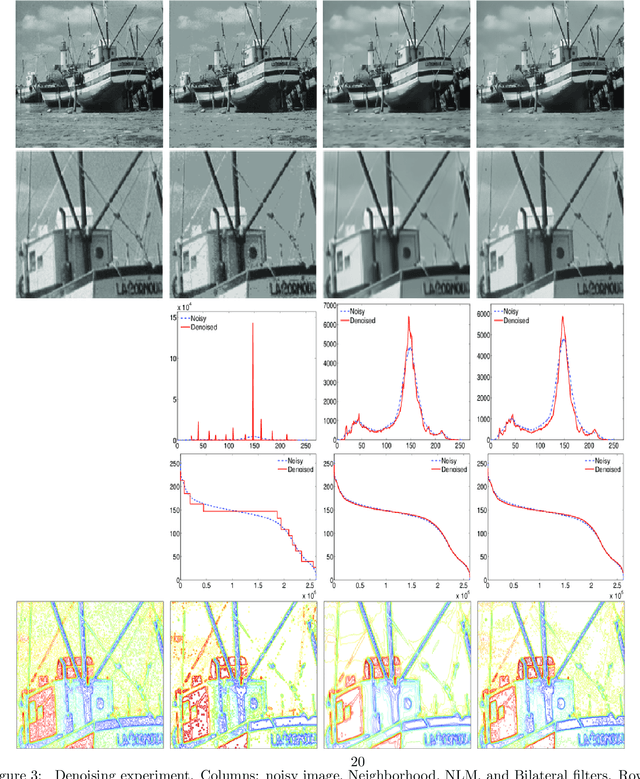
Nonlocal filters are simple and powerful techniques for image denoising. In this paper, we give new insights into the analysis of one kind of them, the Neighborhood filter, by using a classical although not very common transformation: the decreasing rearrangement of a function (the image). Independently of the dimension of the image, we reformulate the Neighborhood filter and its iterative variants as an integral operator defined in a one-dimensional space. The simplicity of this formulation allows to perform a detailed analysis of its properties. Among others, we prove that the filter behaves asymptotically as a shock filter combined with a border diffusive term, responsible for the staircaising effect and the loss of contrast.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge