Non-convex non-local flows for saliency detection

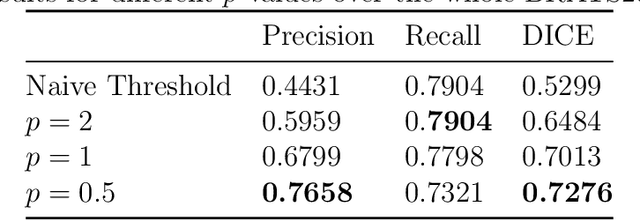
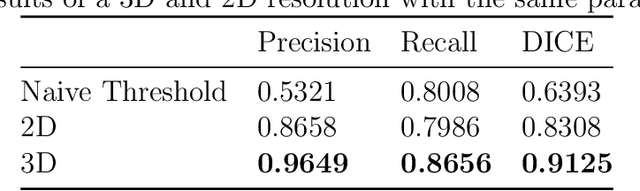
We propose and numerically solve a new variational model for automatic saliency detection in digital images. Using a non-local framework we consider a family of edge preserving functions combined with a new quadratic saliency detection term. Such term defines a constrained bilateral obstacle problem for image classification driven by p-Laplacian operators, including the so-called hyper-Laplacian case (0 < p < 1). The related non-convex non-local reactive flows are then considered and applied for glioblastoma segmentation in magnetic resonance fluid-attenuated inversion recovery (MRI-Flair) images. A fast convolutional kernel based approximated solution is computed. The numerical experiments show how the non-convexity related to the hyperLaplacian operators provides monotonically better results in terms of the standard metrics.

On 1-Laplacian Elliptic Equations Modeling Magnetic Resonance Image Rician Denoising

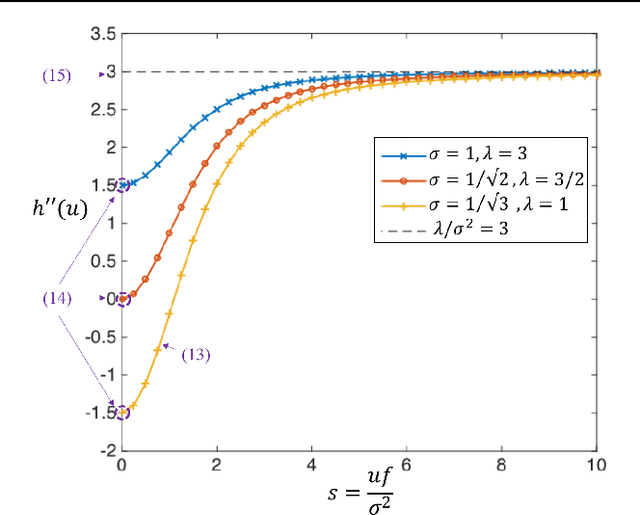
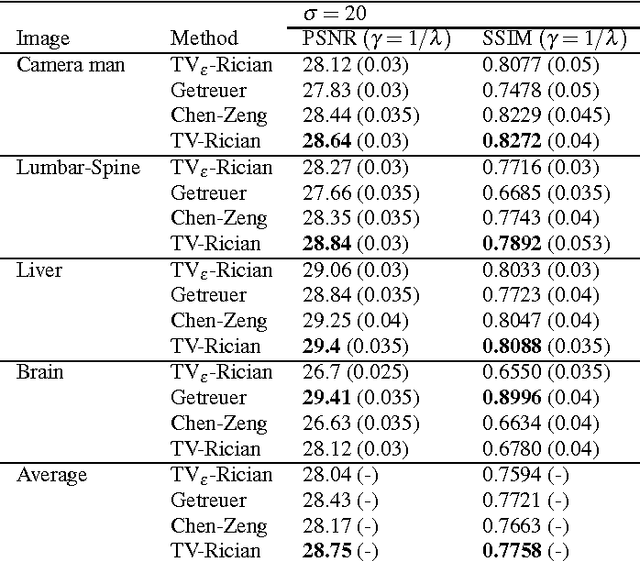
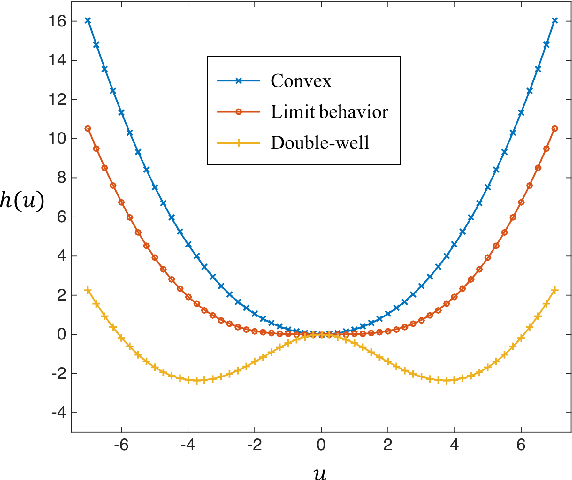
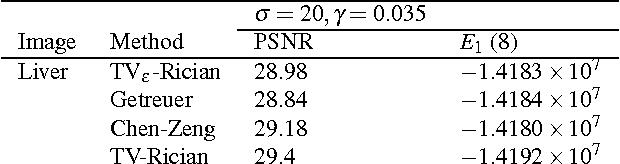
Modeling magnitude Magnetic Resonance Images (MRI) rician denoising in a Bayesian or generalized Tikhonov framework using Total Variation (TV) leads naturally to the consideration of nonlinear elliptic equations. These involve the so called $1$-Laplacian operator and special care is needed to properly formulate the problem. The rician statistics of the data are introduced through a singular equation with a reaction term defined in terms of modified first order Bessel functions. An existence theory is provided here together with other qualitative properties of the solutions. Remarkably, each positive global minimum of the associated functional is one of such solutions. Moreover, we directly solve this non--smooth non--convex minimization problem using a convergent Proximal Point Algorithm. Numerical results based on synthetic and real MRI demonstrate a better performance of the proposed method when compared to previous TV based models for rician denoising which regularize or convexify the problem. Finally, an application on real Diffusion Tensor Images, a strongly affected by rician noise MRI modality, is presented and discussed.

Well-posedness of a nonlinear integro-differential problem and its rearranged formulation

We study the existence and uniqueness of solutions of a nonlinear integro-differential problem which we reformulate introducing the notion of the decreasing rearrangement of the solution. A dimensional reduction of the problem is obtained and a detailed analysis of the properties of the solutions of the model is provided. Finally, a fast numerical method is devised and implemented to show the performance of the model when typical image processing tasks such as filtering and segmentation are performed.