Non-convex non-local flows for saliency detection
Paper and Code
May 23, 2018
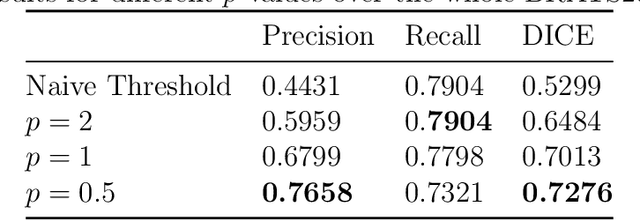

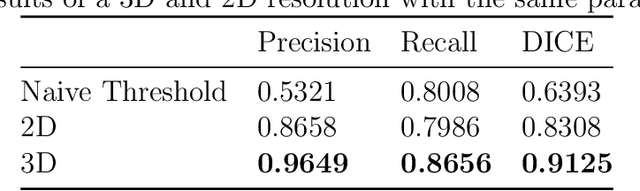
We propose and numerically solve a new variational model for automatic saliency detection in digital images. Using a non-local framework we consider a family of edge preserving functions combined with a new quadratic saliency detection term. Such term defines a constrained bilateral obstacle problem for image classification driven by p-Laplacian operators, including the so-called hyper-Laplacian case (0 < p < 1). The related non-convex non-local reactive flows are then considered and applied for glioblastoma segmentation in magnetic resonance fluid-attenuated inversion recovery (MRI-Flair) images. A fast convolutional kernel based approximated solution is computed. The numerical experiments show how the non-convexity related to the hyperLaplacian operators provides monotonically better results in terms of the standard metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge