On a non-local spectrogram for denoising one-dimensional signals
Paper and Code
Nov 13, 2013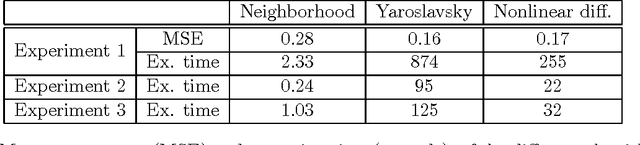
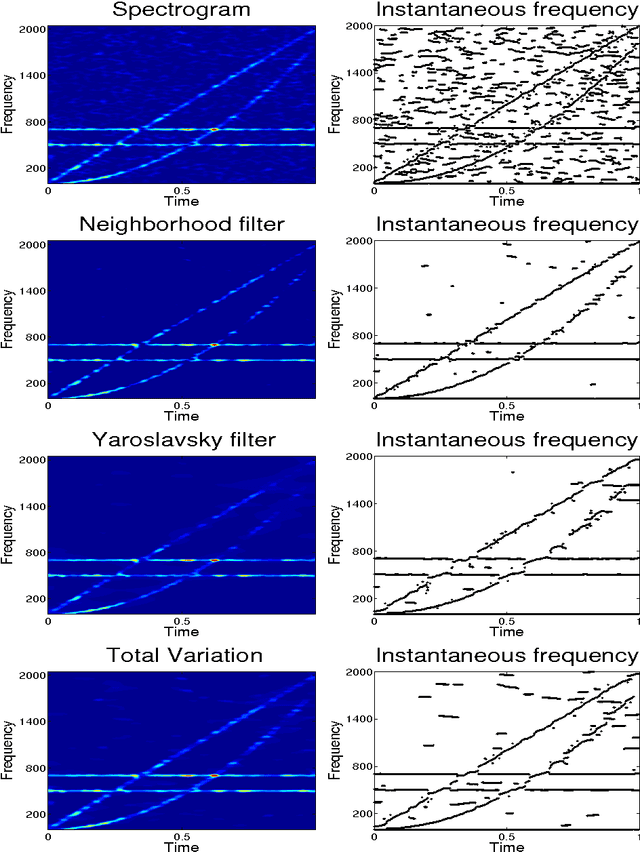
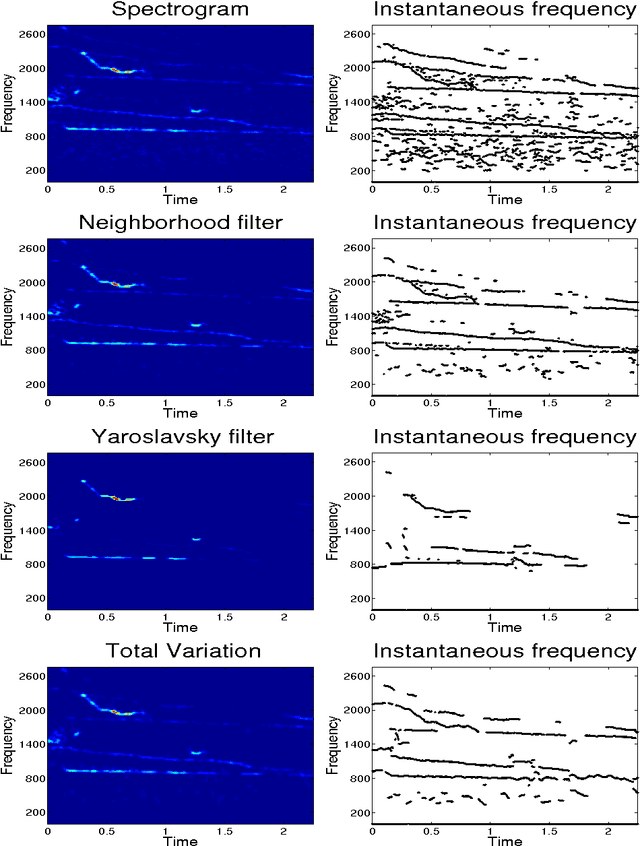
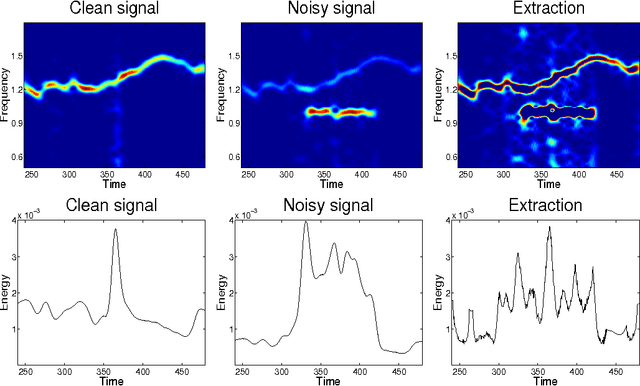
In previous works, we investigated the use of local filters based on partial differential equations (PDE) to denoise one-dimensional signals through the image processing of time-frequency representations, such as the spectrogram. In this image denoising algorithms, the particularity of the image was hardly taken into account. We turn, in this paper, to study the performance of non-local filters, like Neighborhood or Yaroslavsky filters, in the same problem. We show that, for certain iterative schemes involving the Neighborhood filter, the computational time is drastically reduced with respect to Yaroslavsky or nonlinear PDE based filters, while the outputs of the filtering processes are similar. This is heuristically justified by the connection between the (fast) Neighborhood filter applied to a spectrogram and the corresponding Nonlocal Means filter (accurate) applied to the Wigner-Ville distribution of the signal. This correspondence holds only for time-frequency representations of one-dimensional signals, not to usual images, and in this sense the particularity of the image is exploited. We compare though a series of experiments on synthetic and biomedical signals the performance of local and non-local filters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge