A Novel Geometric Framework on Gram Matrix Trajectories for Human Behavior Understanding

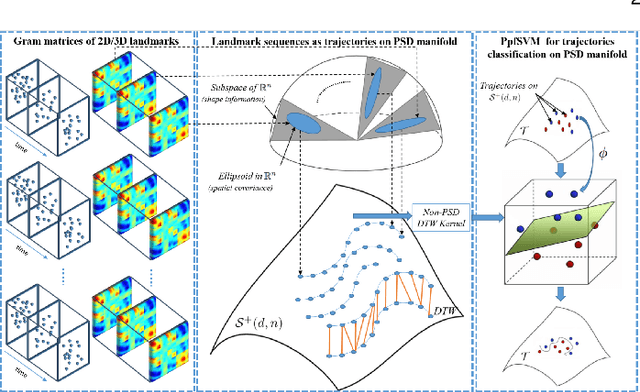
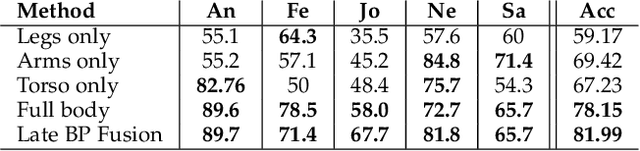
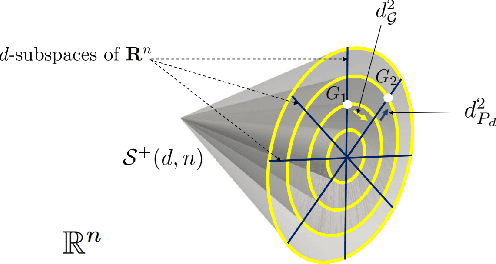
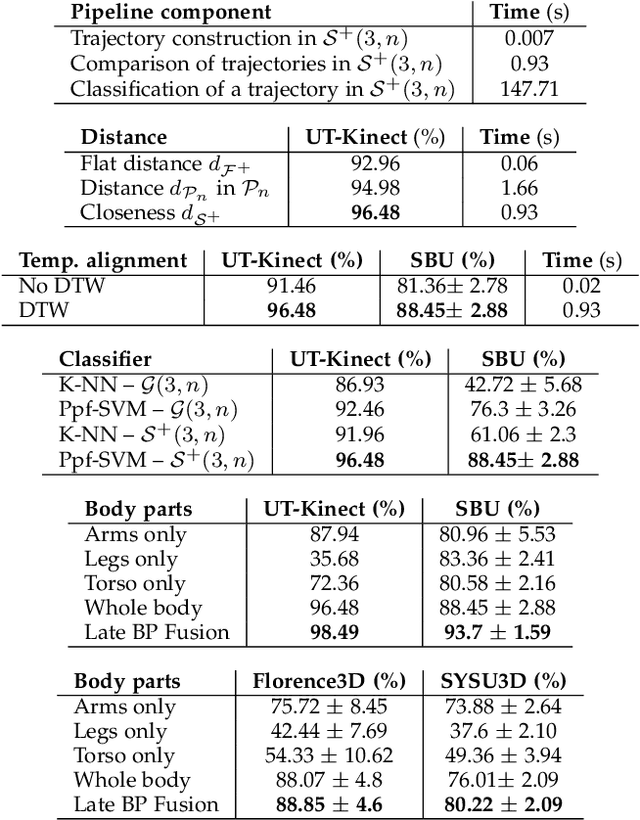
In this paper, we propose a novel space-time geometric representation of human landmark configurations and derive tools for comparison and classification. We model the temporal evolution of landmarks as parametrized trajectories on the Riemannian manifold of positive semidefinite matrices of fixed-rank. Our representation has the benefit to bring naturally a second desirable quantity when comparing shapes, the spatial covariance, in addition to the conventional affine-shape representation. We derived then geometric and computational tools for rate-invariant analysis and adaptive re-sampling of trajectories, grounding on the Riemannian geometry of the underlying manifold. Specifically, our approach involves three steps: (1) landmarks are first mapped into the Riemannian manifold of positive semidefinite matrices of fixed-rank to build time-parameterized trajectories; (2) a temporal warping is performed on the trajectories, providing a geometry-aware (dis-)similarity measure between them; (3) finally, a pairwise proximity function SVM is used to classify them, incorporating the (dis-)similarity measure into the kernel function. We show that such representation and metric achieve competitive results in applications as action recognition and emotion recognition from 3D skeletal data, and facial expression recognition from videos. Experiments have been conducted on several publicly available up-to-date benchmarks.

A Novel Space-Time Representation on the Positive Semidefinite Con for Facial Expression Recognition

In this paper, we study the problem of facial expression recognition using a novel space-time geometric representation. We describe the temporal evolution of facial landmarks as parametrized trajectories on the Riemannian manifold of positive semidefinite matrices of fixed-rank. Our representation has the advantage to bring naturally a second desirable quantity when comparing shapes -- the spatial covariance -- in addition to the conventional affine-shape representation. We derive then geometric and computational tools for rate-invariant analysis and adaptive re-sampling of trajectories, grounding on the Riemannian geometry of the manifold. Specifically, our approach involves three steps: 1) facial landmarks are first mapped into the Riemannian manifold of positive semidefinite matrices of rank 2, to build time-parameterized trajectories; 2) a temporal alignment is performed on the trajectories, providing a geometry-aware (dis-)similarity measure between them; 3) finally, pairwise proximity function SVM (ppfSVM) is used to classify them, incorporating the latter (dis-)similarity measure into the kernel function. We show the effectiveness of the proposed approach on four publicly available benchmarks (CK+, MMI, Oulu-CASIA, and AFEW). The results of the proposed approach are comparable to or better than the state-of-the-art methods when involving only facial landmarks.