VIB is Half Bayes

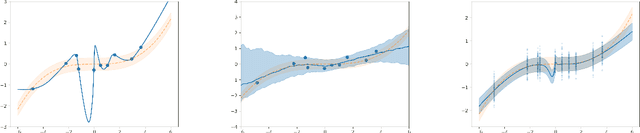
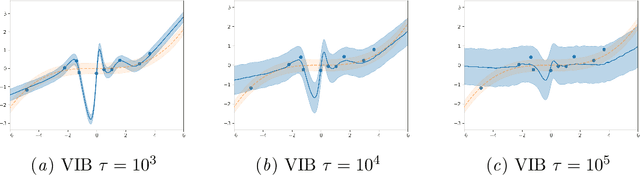
In discriminative settings such as regression and classification there are two random variables at play, the inputs X and the targets Y. Here, we demonstrate that the Variational Information Bottleneck can be viewed as a compromise between fully empirical and fully Bayesian objectives, attempting to minimize the risks due to finite sampling of Y only. We argue that this approach provides some of the benefits of Bayes while requiring only some of the work.

Statistical and Computational Tradeoffs in Stochastic Composite Likelihood

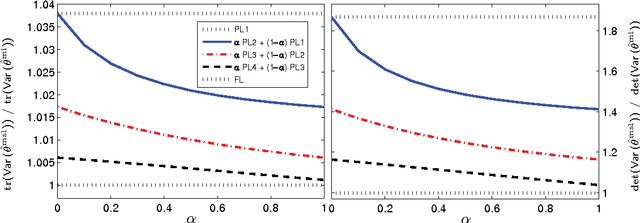
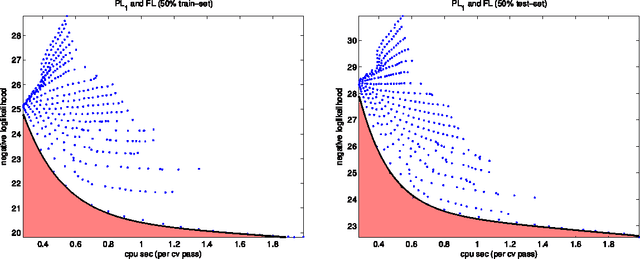
Maximum likelihood estimators are often of limited practical use due to the intensive computation they require. We propose a family of alternative estimators that maximize a stochastic variation of the composite likelihood function. Each of the estimators resolve the computation-accuracy tradeoff differently, and taken together they span a continuous spectrum of computation-accuracy tradeoff resolutions. We prove the consistency of the estimators, provide formulas for their asymptotic variance, statistical robustness, and computational complexity. We discuss experimental results in the context of Boltzmann machines and conditional random fields. The theoretical and experimental studies demonstrate the effectiveness of the estimators when the computational resources are insufficient. They also demonstrate that in some cases reduced computational complexity is associated with robustness thereby increasing statistical accuracy.

Asymptotic Analysis of Generative Semi-Supervised Learning

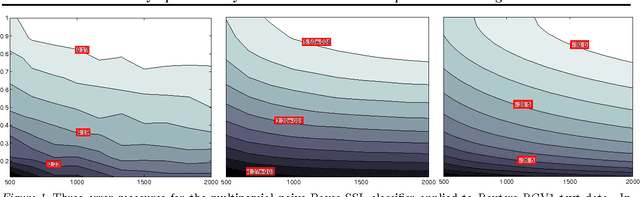
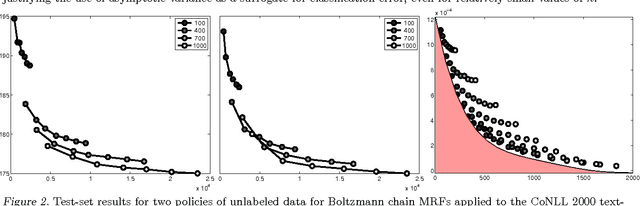
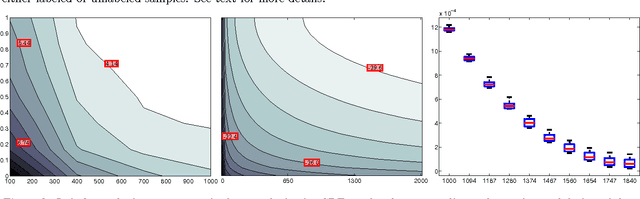
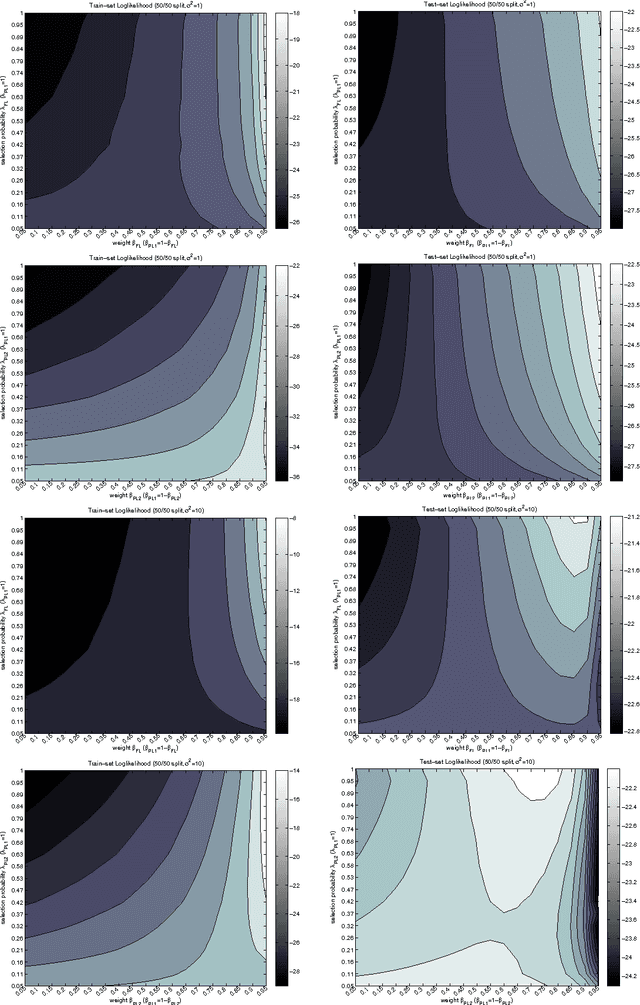
Semisupervised learning has emerged as a popular framework for improving modeling accuracy while controlling labeling cost. Based on an extension of stochastic composite likelihood we quantify the asymptotic accuracy of generative semi-supervised learning. In doing so, we complement distribution-free analysis by providing an alternative framework to measure the value associated with different labeling policies and resolve the fundamental question of how much data to label and in what manner. We demonstrate our approach with both simulation studies and real world experiments using naive Bayes for text classification and MRFs and CRFs for structured prediction in NLP.