Joris Pries
The Berkelmans-Pries Feature Importance Method: A Generic Measure of Informativeness of Features
Jan 11, 2023Abstract:Over the past few years, the use of machine learning models has emerged as a generic and powerful means for prediction purposes. At the same time, there is a growing demand for interpretability of prediction models. To determine which features of a dataset are important to predict a target variable $Y$, a Feature Importance (FI) method can be used. By quantifying how important each feature is for predicting $Y$, irrelevant features can be identified and removed, which could increase the speed and accuracy of a model, and moreover, important features can be discovered, which could lead to valuable insights. A major problem with evaluating FI methods, is that the ground truth FI is often unknown. As a consequence, existing FI methods do not give the exact correct FI values. This is one of the many reasons why it can be hard to properly interpret the results of an FI method. Motivated by this, we introduce a new global approach named the Berkelmans-Pries FI method, which is based on a combination of Shapley values and the Berkelmans-Pries dependency function. We prove that our method has many useful properties, and accurately predicts the correct FI values for several cases where the ground truth FI can be derived in an exact manner. We experimentally show for a large collection of FI methods (468) that existing methods do not have the same useful properties. This shows that the Berkelmans-Pries FI method is a highly valuable tool for analyzing datasets with complex interdependencies.
The Optimal Input-Independent Baseline for Binary Classification: The Dutch Draw
Jan 09, 2023Abstract:Before any binary classification model is taken into practice, it is important to validate its performance on a proper test set. Without a frame of reference given by a baseline method, it is impossible to determine if a score is `good' or `bad'. The goal of this paper is to examine all baseline methods that are independent of feature values and determine which model is the `best' and why. By identifying which baseline models are optimal, a crucial selection decision in the evaluation process is simplified. We prove that the recently proposed Dutch Draw baseline is the best input-independent classifier (independent of feature values) for all positional-invariant measures (independent of sequence order) assuming that the samples are randomly shuffled. This means that the Dutch Draw baseline is the optimal baseline under these intuitive requirements and should therefore be used in practice.
The Dutch Draw: Constructing a Universal Baseline for Binary Prediction Models
Mar 24, 2022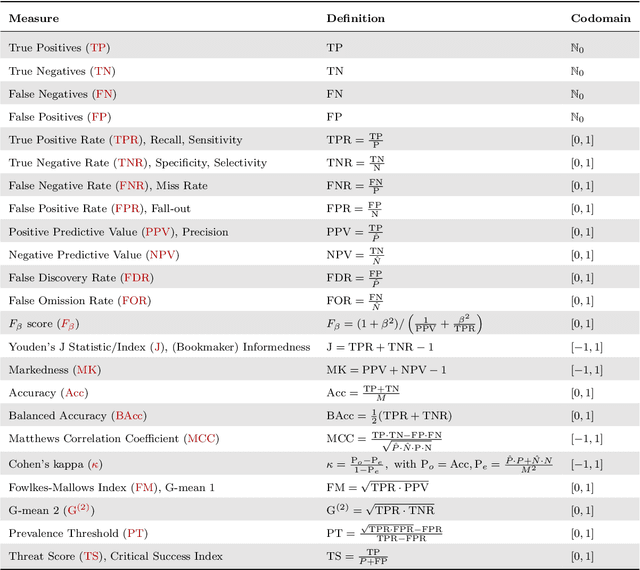
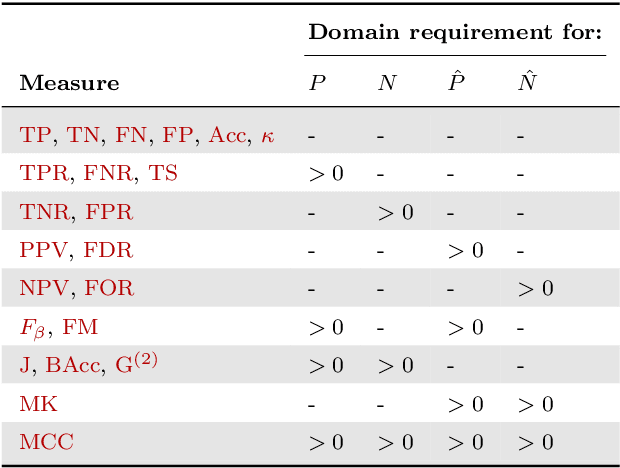

Abstract:Novel prediction methods should always be compared to a baseline to know how well they perform. Without this frame of reference, the performance score of a model is basically meaningless. What does it mean when a model achieves an $F_1$ of 0.8 on a test set? A proper baseline is needed to evaluate the `goodness' of a performance score. Comparing with the latest state-of-the-art model is usually insightful. However, being state-of-the-art can change rapidly when newer models are developed. Contrary to an advanced model, a simple dummy classifier could be used. However, the latter could be beaten too easily, making the comparison less valuable. This paper presents a universal baseline method for all binary classification models, named the Dutch Draw (DD). This approach weighs simple classifiers and determines the best classifier to use as a baseline. We theoretically derive the DD baseline for many commonly used evaluation measures and show that in most situations it reduces to (almost) always predicting either zero or one. Summarizing, the DD baseline is: (1) general, as it is applicable to all binary classification problems; (2) simple, as it is quickly determined without training or parameter-tuning; (3) informative, as insightful conclusions can be drawn from the results. The DD baseline serves two purposes. First, to enable comparisons across research papers by this robust and universal baseline. Secondly, to provide a sanity check during the development process of a prediction model. It is a major warning sign when a model is outperformed by the DD baseline.
The BP Dependency Function: a Generic Measure of Dependence between Random Variables
Mar 23, 2022


Abstract:Measuring and quantifying dependencies between random variables (RV's) can give critical insights into a data-set. Typical questions are: `Do underlying relationships exist?', `Are some variables redundant?', and `Is some target variable $Y$ highly or weakly dependent on variable $X$?' Interestingly, despite the evident need for a general-purpose measure of dependency between RV's, common practice of data analysis is that most data analysts use the Pearson correlation coefficient (PCC) to quantify dependence between RV's, while it is well-recognized that the PCC is essentially a measure for linear dependency only. Although many attempts have been made to define more generic dependency measures, there is yet no consensus on a standard, general-purpose dependency function. In fact, several ideal properties of a dependency function have been proposed, but without much argumentation. Motivated by this, in this paper we will discuss and revise the list of desired properties and propose a new dependency function that meets all these requirements. This general-purpose dependency function provides data analysts a powerful means to quantify the level of dependence between variables. To this end, we also provide Python code to determine the dependency function for use in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge