The Optimal Input-Independent Baseline for Binary Classification: The Dutch Draw

Before any binary classification model is taken into practice, it is important to validate its performance on a proper test set. Without a frame of reference given by a baseline method, it is impossible to determine if a score is `good' or `bad'. The goal of this paper is to examine all baseline methods that are independent of feature values and determine which model is the `best' and why. By identifying which baseline models are optimal, a crucial selection decision in the evaluation process is simplified. We prove that the recently proposed Dutch Draw baseline is the best input-independent classifier (independent of feature values) for all positional-invariant measures (independent of sequence order) assuming that the samples are randomly shuffled. This means that the Dutch Draw baseline is the optimal baseline under these intuitive requirements and should therefore be used in practice.

The Dutch Draw: Constructing a Universal Baseline for Binary Prediction Models

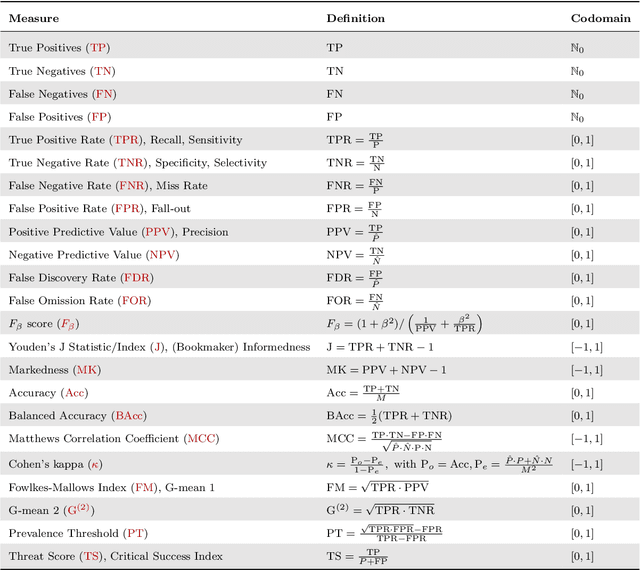
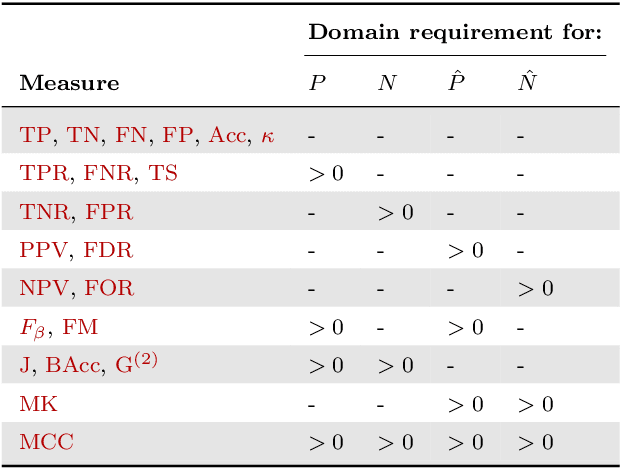
Novel prediction methods should always be compared to a baseline to know how well they perform. Without this frame of reference, the performance score of a model is basically meaningless. What does it mean when a model achieves an $F_1$ of 0.8 on a test set? A proper baseline is needed to evaluate the `goodness' of a performance score. Comparing with the latest state-of-the-art model is usually insightful. However, being state-of-the-art can change rapidly when newer models are developed. Contrary to an advanced model, a simple dummy classifier could be used. However, the latter could be beaten too easily, making the comparison less valuable. This paper presents a universal baseline method for all binary classification models, named the Dutch Draw (DD). This approach weighs simple classifiers and determines the best classifier to use as a baseline. We theoretically derive the DD baseline for many commonly used evaluation measures and show that in most situations it reduces to (almost) always predicting either zero or one. Summarizing, the DD baseline is: (1) general, as it is applicable to all binary classification problems; (2) simple, as it is quickly determined without training or parameter-tuning; (3) informative, as insightful conclusions can be drawn from the results. The DD baseline serves two purposes. First, to enable comparisons across research papers by this robust and universal baseline. Secondly, to provide a sanity check during the development process of a prediction model. It is a major warning sign when a model is outperformed by the DD baseline.