Predicting Water Temperature Dynamics of Unmonitored Lakes with Meta Transfer Learning

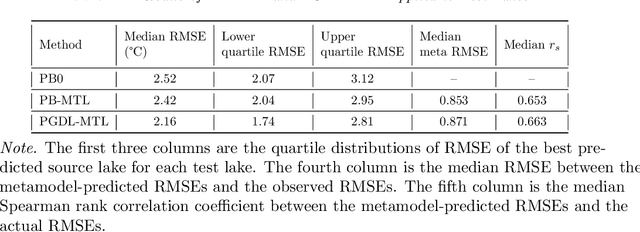
Most environmental data come from a minority of well-observed sites. An ongoing challenge in the environmental sciences is transferring knowledge from monitored sites to unobserved sites. Here, we demonstrate a novel transfer learning framework that accurately predicts temperature in unobserved lakes (targets) by borrowing models from highly observed lakes (sources). This method, Meta Transfer Learning (MTL), builds a meta-learning model to predict transfer performance from candidate source models to targets using lake attributes and candidates' past performance. We constructed source models at 145 well-observed lakes using calibrated process-based modeling (PB) and a recently developed approach called process-guided deep learning (PGDL). We applied MTL to either PB or PGDL source models (PB-MTL or PGDL-MTL, respectively) to predict temperatures in 305 target lakes treated as unobserved in the Upper Midwestern United States. We show significantly improved performance relative to the uncalibrated process-based General Lake Model, where the median RMSE for the target lakes is $2.52^{\circ}C$. PB-MTL yielded a median RMSE of $2.43^{\circ}C$; PGDL-MTL yielded $2.16^{\circ}C$; and a PGDL-MTL ensemble of nine sources per target yielded $1.88^{\circ}C$. For sparsely observed target lakes, PGDL-MTL often outperformed PGDL models trained on the target lakes themselves. Differences in maximum depth between the source and target were consistently the most important predictors. Our approach readily scales to thousands of lakes in the Midwestern United States, demonstrating that MTL with meaningful predictor variables and high-quality source models is a promising approach for many kinds of unmonitored systems and environmental variables.

Physics-Guided Architecture (PGA) of Neural Networks for Quantifying Uncertainty in Lake Temperature Modeling

To simultaneously address the rising need of expressing uncertainties in deep learning models along with producing model outputs which are consistent with the known scientific knowledge, we propose a novel physics-guided architecture (PGA) of neural networks in the context of lake temperature modeling where the physical constraints are hard coded in the neural network architecture. This allows us to integrate such models with state of the art uncertainty estimation approaches such as Monte Carlo (MC) Dropout without sacrificing the physical consistency of our results. We demonstrate the effectiveness of our approach in ensuring better generalizability as well as physical consistency in MC estimates over data collected from Lake Mendota in Wisconsin and Falling Creek Reservoir in Virginia, even with limited training data. We further show that our MC estimates correctly match the distribution of ground-truth observations, thus making the PGA paradigm amenable to physically grounded uncertainty quantification.