Heterogeneous Stream-reservoir Graph Networks with Data Assimilation

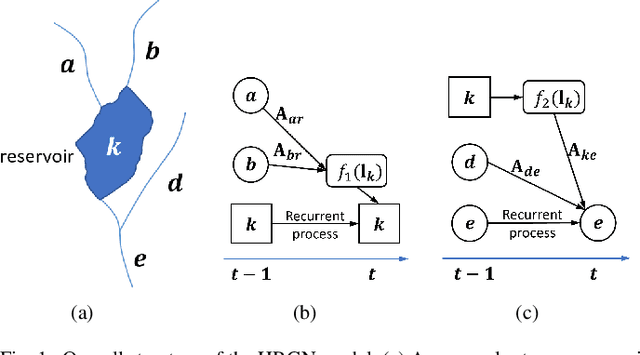
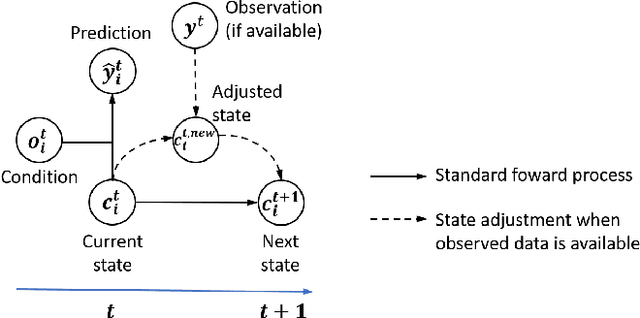
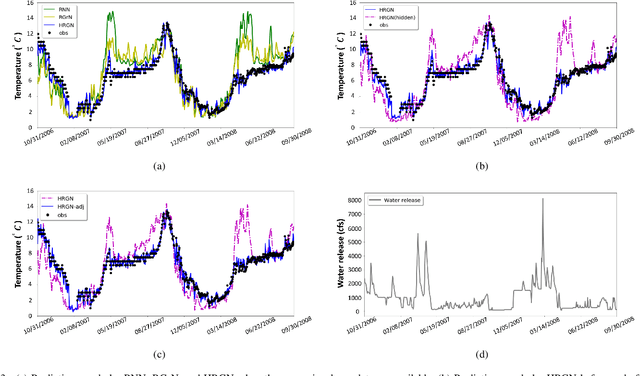
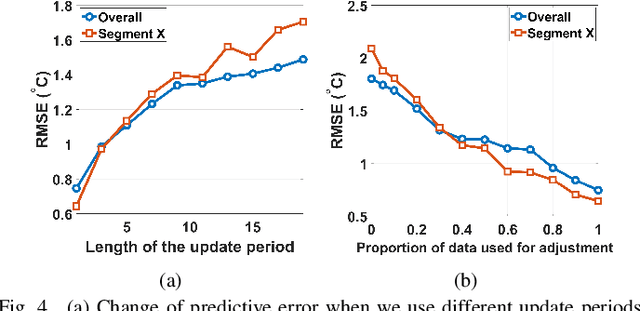
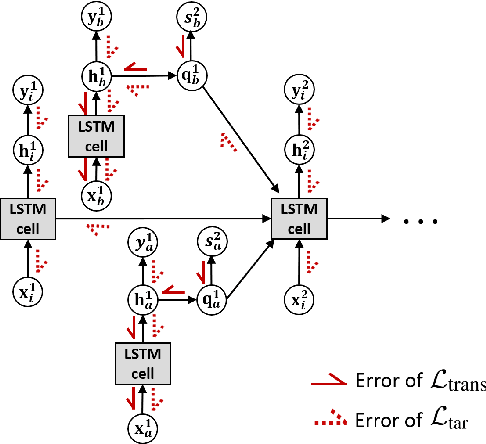
Accurate prediction of water temperature in streams is critical for monitoring and understanding biogeochemical and ecological processes in streams. Stream temperature is affected by weather patterns (such as solar radiation) and water flowing through the stream network. Additionally, stream temperature can be substantially affected by water releases from man-made reservoirs to downstream segments. In this paper, we propose a heterogeneous recurrent graph model to represent these interacting processes that underlie stream-reservoir networks and improve the prediction of water temperature in all river segments within a network. Because reservoir release data may be unavailable for certain reservoirs, we further develop a data assimilation mechanism to adjust the deep learning model states to correct for the prediction bias caused by reservoir releases. A well-trained temporal modeling component is needed in order to use adjusted states to improve future predictions. Hence, we also introduce a simulation-based pre-training strategy to enhance the model training. Our evaluation for the Delaware River Basin has demonstrated the superiority of our proposed method over multiple existing methods. We have extensively studied the effect of the data assimilation mechanism under different scenarios. Moreover, we show that the proposed method using the pre-training strategy can still produce good predictions even with limited training data.

Graph-based Reinforcement Learning for Active Learning in Real Time: An Application in Modeling River Networks

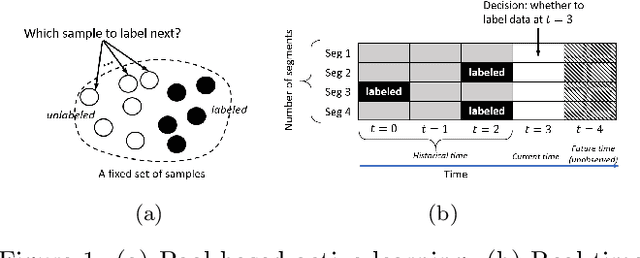
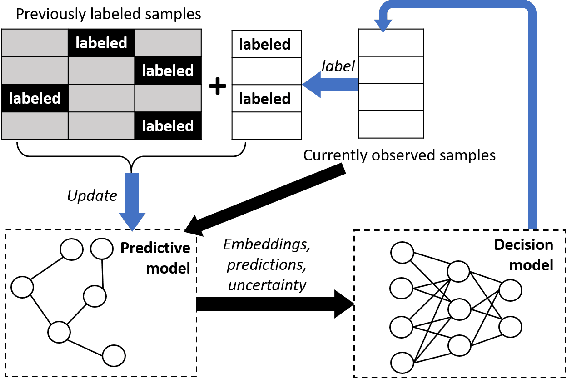
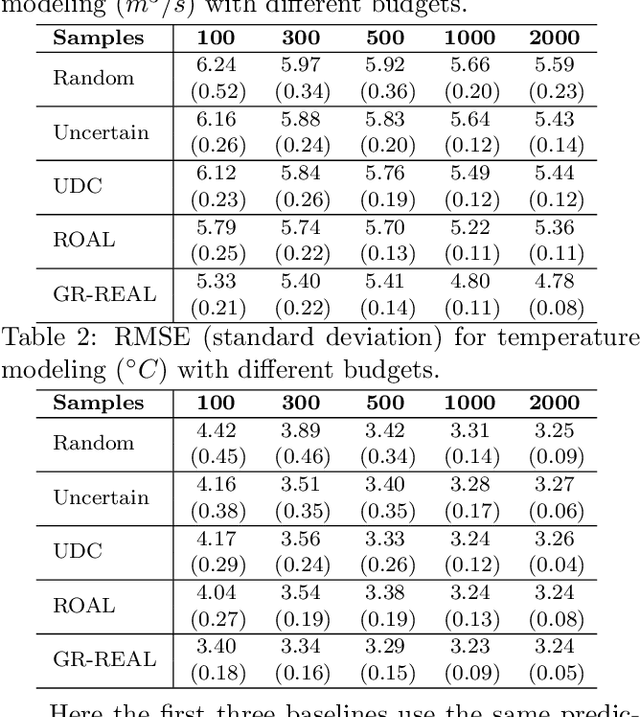
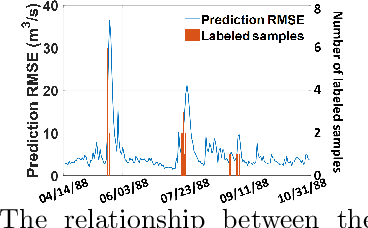
Effective training of advanced ML models requires large amounts of labeled data, which is often scarce in scientific problems given the substantial human labor and material cost to collect labeled data. This poses a challenge on determining when and where we should deploy measuring instruments (e.g., in-situ sensors) to collect labeled data efficiently. This problem differs from traditional pool-based active learning settings in that the labeling decisions have to be made immediately after we observe the input data that come in a time series. In this paper, we develop a real-time active learning method that uses the spatial and temporal contextual information to select representative query samples in a reinforcement learning framework. To reduce the need for large training data, we further propose to transfer the policy learned from simulation data which is generated by existing physics-based models. We demonstrate the effectiveness of the proposed method by predicting streamflow and water temperature in the Delaware River Basin given a limited budget for collecting labeled data. We further study the spatial and temporal distribution of selected samples to verify the ability of this method in selecting informative samples over space and time.

Physics-Guided Recurrent Graph Networks for Predicting Flow and Temperature in River Networks

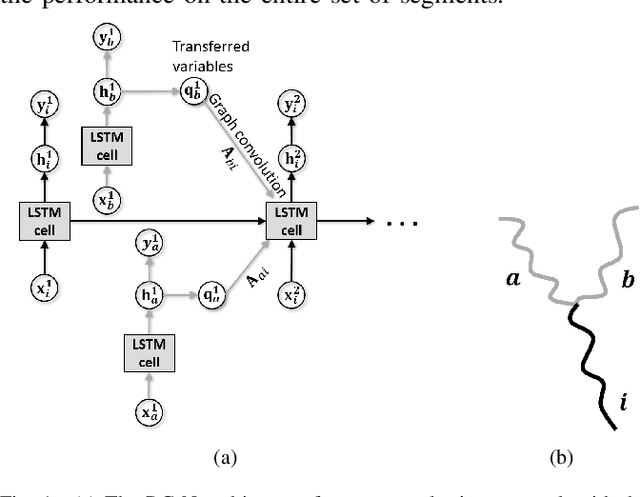
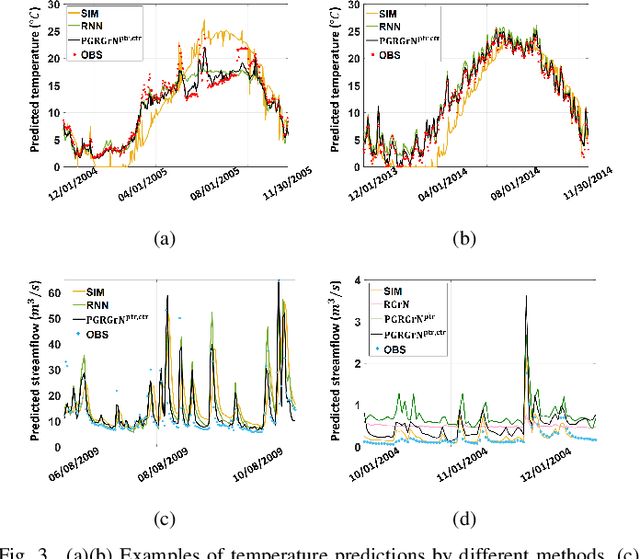
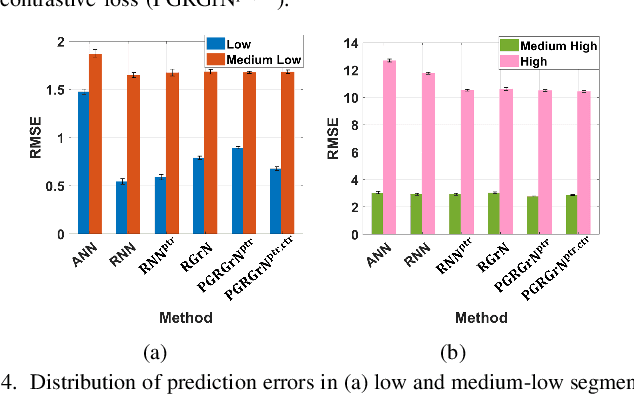
This paper proposes a physics-guided machine learning approach that combines advanced machine learning models and physics-based models to improve the prediction of water flow and temperature in river networks. We first build a recurrent graph network model to capture the interactions among multiple segments in the river network. Then we present a pre-training technique which transfers knowledge from physics-based models to initialize the machine learning model and learn the physics of streamflow and thermodynamics. We also propose a new loss function that balances the performance over different river segments. We demonstrate the effectiveness of the proposed method in predicting temperature and streamflow in a subset of the Delaware River Basin. In particular, we show that the proposed method brings a 33\%/14\% improvement over the state-of-the-art physics-based model and 24\%/14\% over traditional machine learning models (e.g., Long-Short Term Memory Neural Network) in temperature/streamflow prediction using very sparse (0.1\%) observation data for training. The proposed method has also been shown to produce better performance when generalized to different seasons or river segments with different streamflow ranges.

Physics Guided RNNs for Modeling Dynamical Systems: A Case Study in Simulating Lake Temperature Profiles

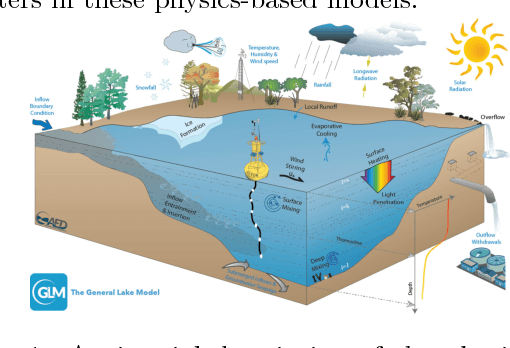
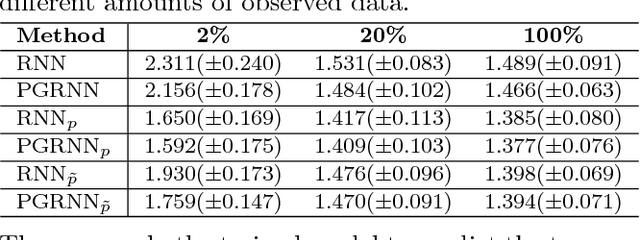
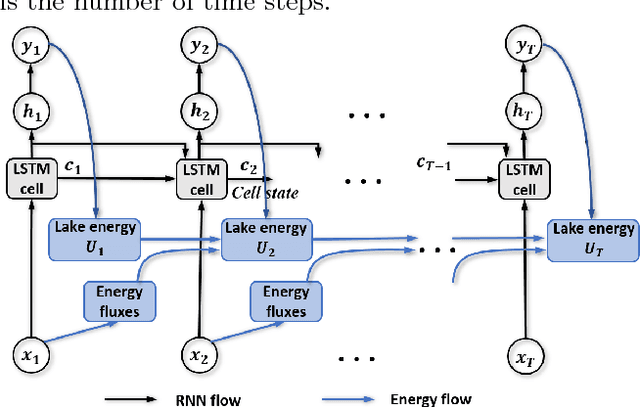
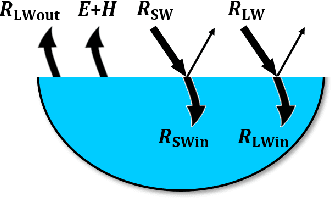
This paper proposes a physics-guided recurrent neural network model (PGRNN) that combines RNNs and physics-based models to leverage their complementary strengths and improve the modeling of physical processes. Specifically, we show that a PGRNN can improve prediction accuracy over that of physical models, while generating outputs consistent with physical laws, and achieving good generalizability. Standard RNNs, even when producing superior prediction accuracy, often produce physically inconsistent results and lack generalizability. We further enhance this approach by using a pre-training method that leverages the simulated data from a physics-based model to address the scarcity of observed data. The PGRNN has the flexibility to incorporate additional physical constraints and we incorporate a density-depth relationship. Both enhancements further improve PGRNN performance. Although we present and evaluate this methodology in the context of modeling the dynamics of temperature in lakes, it is applicable more widely to a range of scientific and engineering disciplines where mechanistic (also known as process-based) models are used, e.g., power engineering, climate science, materials science, computational chemistry, and biomedicine.

Physics-guided Neural Networks (PGNN): An Application in Lake Temperature Modeling

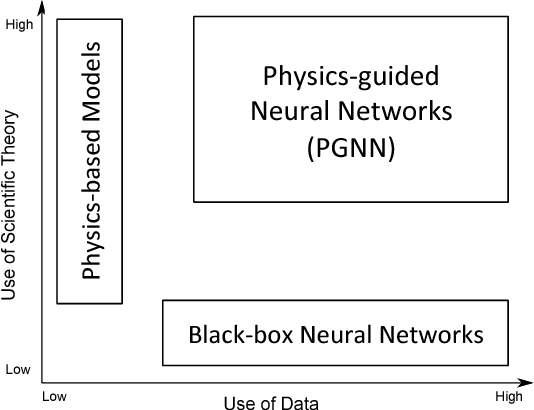
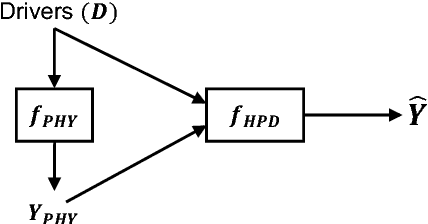
This paper introduces a novel framework for combining scientific knowledge of physics-based models with neural networks to advance scientific discovery. This framework, termed as physics-guided neural network (PGNN), leverages the output of physics-based model simulations along with observational features to generate predictions using a neural network architecture. Further, this paper presents a novel framework for using physics-based loss functions in the learning objective of neural networks, to ensure that the model predictions not only show lower errors on the training set but are also scientifically consistent with the known physics on the unlabeled set. We illustrate the effectiveness of PGNN for the problem of lake temperature modeling, where physical relationships between the temperature, density, and depth of water are used to design a physics-based loss function. By using scientific knowledge to guide the construction and learning of neural networks, we are able to show that the proposed framework ensures better generalizability as well as scientific consistency of results.