Does a Large Language Model Really Speak in Human-Like Language?

Large Language Models (LLMs) have recently emerged, attracting considerable attention due to their ability to generate highly natural, human-like text. This study compares the latent community structures of LLM-generated text and human-written text within a hypothesis testing procedure. Specifically, we analyze three text sets: original human-written texts ($\mathcal{O}$), their LLM-paraphrased versions ($\mathcal{G}$), and a twice-paraphrased set ($\mathcal{S}$) derived from $\mathcal{G}$. Our analysis addresses two key questions: (1) Is the difference in latent community structures between $\mathcal{O}$ and $\mathcal{G}$ the same as that between $\mathcal{G}$ and $\mathcal{S}$? (2) Does $\mathcal{G}$ become more similar to $\mathcal{O}$ as the LLM parameter controlling text variability is adjusted? The first question is based on the assumption that if LLM-generated text truly resembles human language, then the gap between the pair ($\mathcal{O}$, $\mathcal{G}$) should be similar to that between the pair ($\mathcal{G}$, $\mathcal{S}$), as both pairs consist of an original text and its paraphrase. The second question examines whether the degree of similarity between LLM-generated and human text varies with changes in the breadth of text generation. To address these questions, we propose a statistical hypothesis testing framework that leverages the fact that each text has corresponding parts across all datasets due to their paraphrasing relationship. This relationship enables the mapping of one dataset's relative position to another, allowing two datasets to be mapped to a third dataset. As a result, both mapped datasets can be quantified with respect to the space characterized by the third dataset, facilitating a direct comparison between them. Our results indicate that GPT-generated text remains distinct from human-authored text.

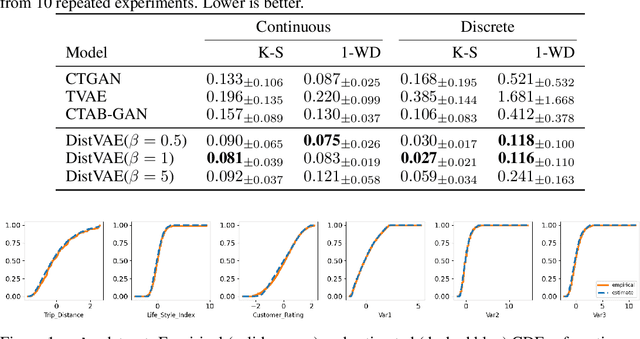
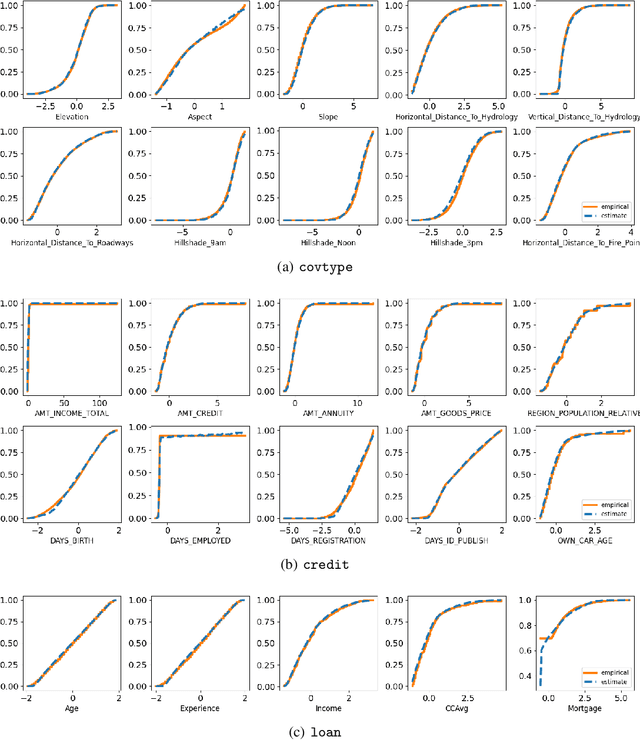
Masked Language Modeling Becomes Conditional Density Estimation for Tabular Data Synthesis

In this paper, our goal is to generate synthetic data for heterogeneous (mixed-type) tabular datasets with high machine learning utility (MLu). Given that the MLu performance relies on accurately approximating the conditional distributions, we focus on devising a synthetic data generation method based on conditional distribution estimation. We propose a novel synthetic data generation method, MaCoDE, by redefining the multi-class classification task of Masked Language Modeling (MLM) as histogram-based non-parametric conditional density estimation. Our proposed method enables estimating conditional densities across arbitrary combinations of target and conditional variables. Furthermore, we demonstrate that our proposed method bridges the theoretical gap between distributional learning and MLM. To validate the effectiveness of our proposed model, we conduct synthetic data generation experiments on 10 real-world datasets. Given the analogy between predicting masked input tokens in MLM and missing data imputation, we also evaluate the performance of multiple imputations on incomplete datasets with various missing data mechanisms. Moreover, our proposed model offers the advantage of enabling adjustments to data privacy levels without requiring re-training.

Improving SMOTE via Fusing Conditional VAE for Data-adaptive Noise Filtering

Recent advances in a generative neural network model extend the development of data augmentation methods. However, the augmentation methods based on the modern generative models fail to achieve notable performance for class imbalance data compared to the conventional model, the SMOTE. We investigate the problem of the generative model for imbalanced classification and introduce a framework to enhance the SMOTE algorithm using Variational Autoencoders (VAE). Our approach systematically quantifies the density of data points in a low-dimensional latent space using the VAE, simultaneously incorporating information on class labels and classification difficulty. Then, the data points potentially degrading the augmentation are systematically excluded, and the neighboring observations are directly augmented on the data space. Empirical studies on several imbalanced datasets represent that this simple process innovatively improves the conventional SMOTE algorithm over the deep learning models. Consequently, we conclude that the selection of minority data and the interpolation in the data space are beneficial for imbalanced classification problems with a relatively small number of data points.

Unicorn: U-Net for Sea Ice Forecasting with Convolutional Neural Ordinary Differential Equations

Sea ice at the North Pole is vital to global climate dynamics. However, accurately forecasting sea ice poses a significant challenge due to the intricate interaction among multiple variables. Leveraging the capability to integrate multiple inputs and powerful performances seamlessly, many studies have turned to neural networks for sea ice forecasting. This paper introduces a novel deep architecture named Unicorn, designed to forecast weekly sea ice. Our model integrates multiple time series images within its architecture to enhance its forecasting performance. Moreover, we incorporate a bottleneck layer within the U-Net architecture, serving as neural ordinary differential equations with convolution operations, to capture the spatiotemporal dynamics of latent variables. Through real data analysis with datasets spanning from 1998 to 2021, our proposed model demonstrates significant improvements over state-of-the-art models in the sea ice concentration forecasting task. It achieves an average MAE improvement of 12% compared to benchmark models. Additionally, our method outperforms existing approaches in sea ice extent forecasting, achieving a classification performance improvement of approximately 18%. These experimental results show the superiority of our proposed model.

Balanced Marginal and Joint Distributional Learning via Mixture Cramer-Wold Distance

In the process of training a generative model, it becomes essential to measure the discrepancy between two high-dimensional probability distributions: the generative distribution and the ground-truth distribution of the observed dataset. Recently, there has been growing interest in an approach that involves slicing high-dimensional distributions, with the Cramer-Wold distance emerging as a promising method. However, we have identified that the Cramer-Wold distance primarily focuses on joint distributional learning, whereas understanding marginal distributional patterns is crucial for effective synthetic data generation. In this paper, we introduce a novel measure of dissimilarity, the mixture Cramer-Wold distance. This measure enables us to capture both marginal and joint distributional information simultaneously, as it incorporates a mixture measure with point masses on standard basis vectors. Building upon the mixture Cramer-Wold distance, we propose a new generative model called CWDAE (Cramer-Wold Distributional AutoEncoder), which shows remarkable performance in generating synthetic data when applied to real tabular datasets. Furthermore, our model offers the flexibility to adjust the level of data privacy with ease.

Joint Distributional Learning via Cramer-Wold Distance

The assumption of conditional independence among observed variables, primarily used in the Variational Autoencoder (VAE) decoder modeling, has limitations when dealing with high-dimensional datasets or complex correlation structures among observed variables. To address this issue, we introduced the Cramer-Wold distance regularization, which can be computed in a closed-form, to facilitate joint distributional learning for high-dimensional datasets. Additionally, we introduced a two-step learning method to enable flexible prior modeling and improve the alignment between the aggregated posterior and the prior distribution. Furthermore, we provide theoretical distinctions from existing methods within this category. To evaluate the synthetic data generation performance of our proposed approach, we conducted experiments on high-dimensional datasets with multiple categorical variables. Given that many readily available datasets and data science applications involve such datasets, our experiments demonstrate the effectiveness of our proposed methodology.

Interpretable Water Level Forecaster with Spatiotemporal Causal Attention Mechanisms

Forecasting the water level of the Han river is important to control traffic and avoid natural disasters. There are many variables related to the Han river and they are intricately connected. In this work, we propose a novel transformer that exploits the causal relationship based on the prior knowledge among the variables and forecasts the water level at the Jamsu bridge in the Han river. Our proposed model considers both spatial and temporal causation by formalizing the causal structure as a multilayer network and using masking methods. Due to this approach, we can have interpretability that consistent with prior knowledge. In real data analysis, we use the Han river dataset from 2016 to 2021 and compare the proposed model with deep learning models.

Uniform Pessimistic Risk and Optimal Portfolio

The optimality of allocating assets has been widely discussed with the theoretical analysis of risk measures. Pessimism is one of the most attractive approaches beyond the conventional optimal portfolio model, and the $\alpha$-risk plays a crucial role in deriving a broad class of pessimistic optimal portfolios. However, estimating an optimal portfolio assessed by a pessimistic risk is still challenging due to the absence of an available estimation model and a computational algorithm. In this study, we propose a version of integrated $\alpha$-risk called the uniform pessimistic risk and the computational algorithm to obtain an optimal portfolio based on the risk. Further, we investigate the theoretical properties of the proposed risk in view of three different approaches: multiple quantile regression, the proper scoring rule, and distributionally robust optimization. Also, the uniform pessimistic risk is applied to estimate the pessimistic optimal portfolio models for the Korean stock market and compare the result of the real data analysis. It is empirically confirmed that the proposed pessimistic portfolio presents a more robust performance than others when the stock market is unstable.

Causally Disentangled Generative Variational AutoEncoder

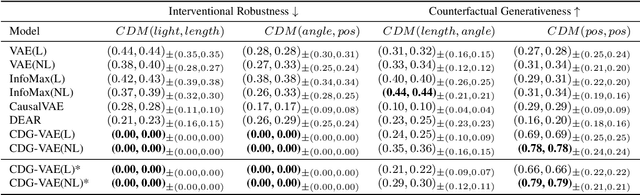
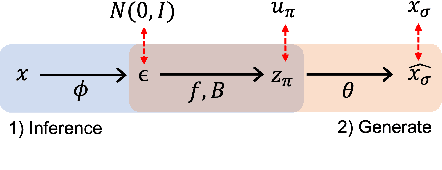
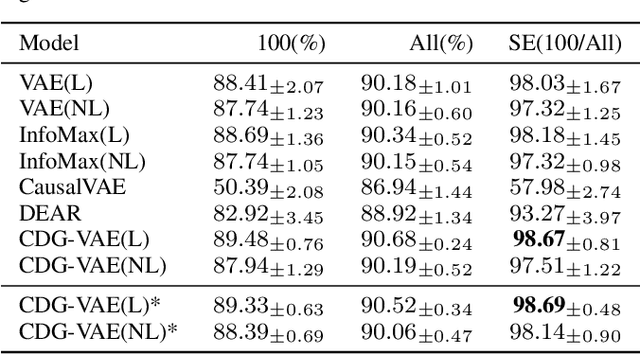
We propose a new supervised learning method for Variational AutoEncoder (VAE) which has a causally disentangled representation and achieves the causally disentangled generation (CDG) simultaneously. In this paper, CDG is defined as a generative model able to decode an output precisely according to the causally disentangled representation. We found that the supervised regularization of the encoder is not enough to obtain a generative model with CDG. Consequently, we explore sufficient and necessary conditions for the decoder and the causal effect to achieve CDG. Moreover, we propose a generalized metric measuring how a model is causally disentangled generative. Numerical results with the image and tabular datasets corroborate our arguments.

Distributional Variational AutoEncoder To Infinite Quantiles and Beyond Gaussianity

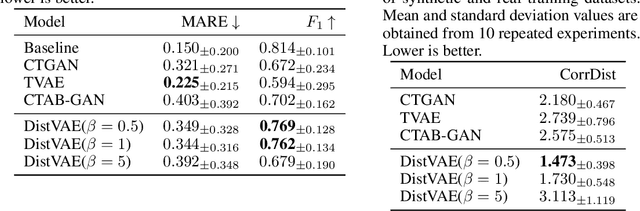
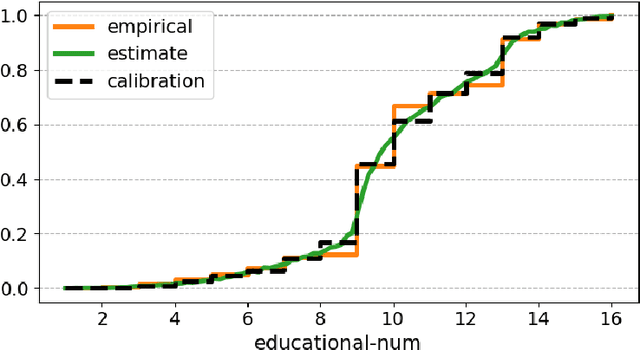
The Gaussianity assumption has been pointed out as the main limitation of the Variational AutoEncoder (VAE) in spite of its usefulness in computation. To improve the distributional capacity (i.e., expressive power of distributional family) of the VAE, we propose a new VAE learning method with a nonparametric distributional assumption on its generative model. By estimating an infinite number of conditional quantiles, our proposed VAE model directly estimates the conditional cumulative distribution function, and we call this approach distributional learning of the VAE. Furthermore, by adopting the continuous ranked probability score (CRPS) loss, our proposed learning method becomes computationally tractable. To evaluate how well the underlying distribution of the dataset is captured, we apply our model for synthetic data generation based on inverse transform sampling. Numerical results with real tabular datasets corroborate our arguments.