Distributional Variational AutoEncoder To Infinite Quantiles and Beyond Gaussianity

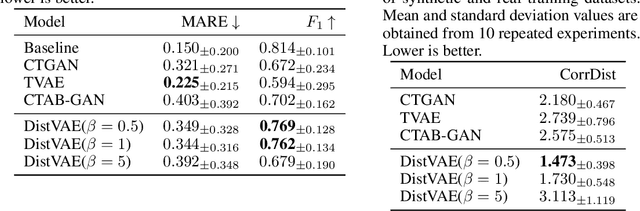
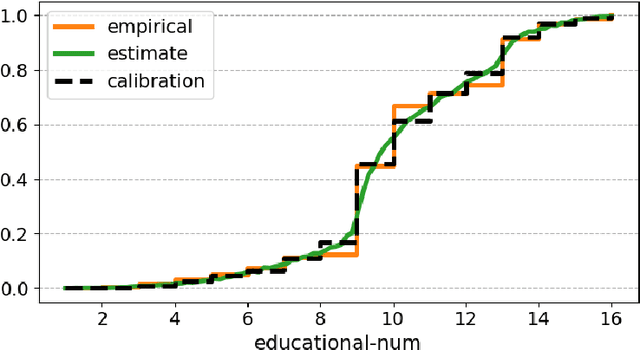
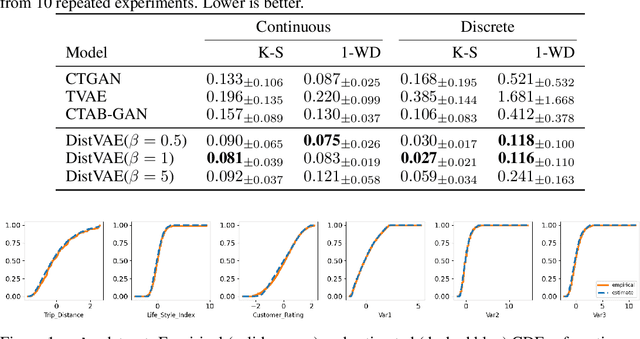
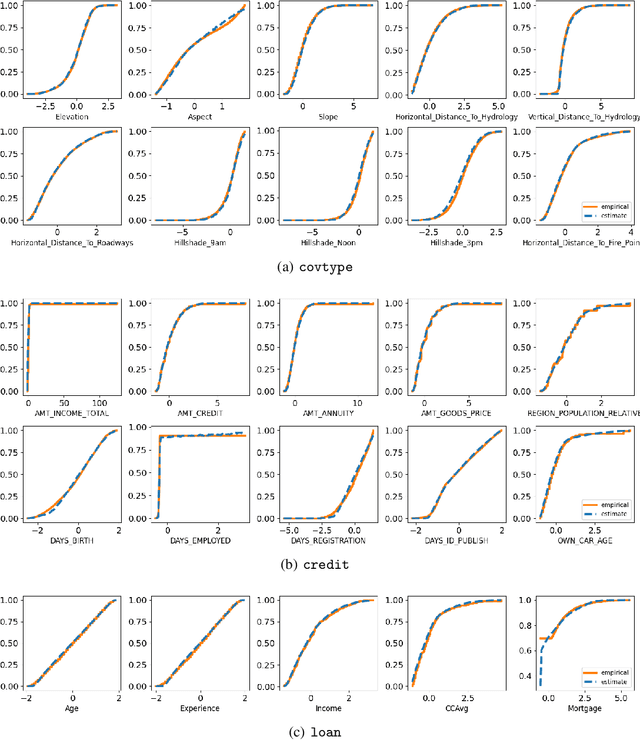
The Gaussianity assumption has been pointed out as the main limitation of the Variational AutoEncoder (VAE) in spite of its usefulness in computation. To improve the distributional capacity (i.e., expressive power of distributional family) of the VAE, we propose a new VAE learning method with a nonparametric distributional assumption on its generative model. By estimating an infinite number of conditional quantiles, our proposed VAE model directly estimates the conditional cumulative distribution function, and we call this approach distributional learning of the VAE. Furthermore, by adopting the continuous ranked probability score (CRPS) loss, our proposed learning method becomes computationally tractable. To evaluate how well the underlying distribution of the dataset is captured, we apply our model for synthetic data generation based on inverse transform sampling. Numerical results with real tabular datasets corroborate our arguments.