Robust Loss Functions for Training Decision Trees with Noisy Labels

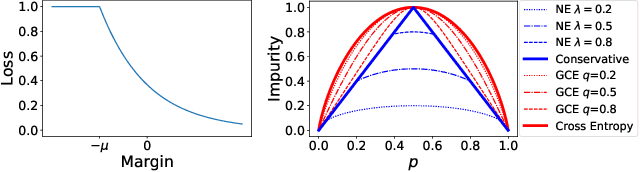
We consider training decision trees using noisily labeled data, focusing on loss functions that can lead to robust learning algorithms. Our contributions are threefold. First, we offer novel theoretical insights on the robustness of many existing loss functions in the context of decision tree learning. We show that some of the losses belong to a class of what we call conservative losses, and the conservative losses lead to an early stopping behavior during training and noise-tolerant predictions during testing. Second, we introduce a framework for constructing robust loss functions, called distribution losses. These losses apply percentile-based penalties based on an assumed margin distribution, and they naturally allow adapting to different noise rates via a robustness parameter. In particular, we introduce a new loss called the negative exponential loss, which leads to an efficient greedy impurity-reduction learning algorithm. Lastly, our experiments on multiple datasets and noise settings validate our theoretical insight and the effectiveness of our adaptive negative exponential loss.

Positive-Unlabeled Learning using Random Forests via Recursive Greedy Risk Minimization

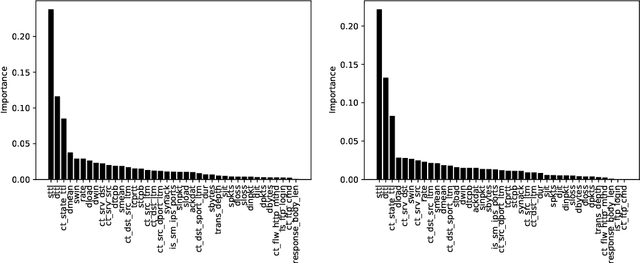
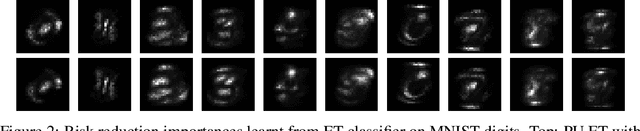
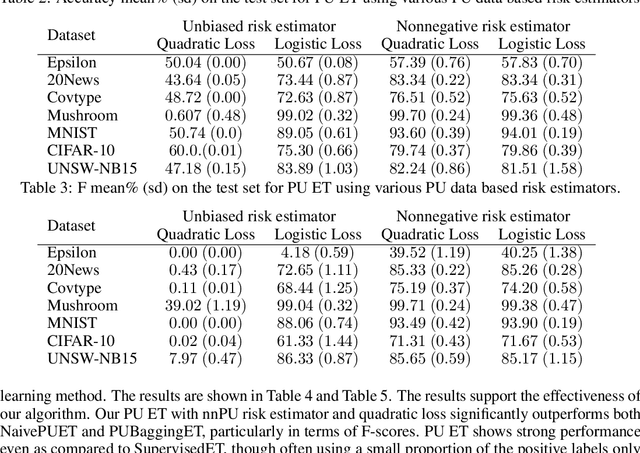
The need to learn from positive and unlabeled data, or PU learning, arises in many applications and has attracted increasing interest. While random forests are known to perform well on many tasks with positive and negative data, recent PU algorithms are generally based on deep neural networks, and the potential of tree-based PU learning is under-explored. In this paper, we propose new random forest algorithms for PU-learning. Key to our approach is a new interpretation of decision tree algorithms for positive and negative data as \emph{recursive greedy risk minimization algorithms}. We extend this perspective to the PU setting to develop new decision tree learning algorithms that directly minimizes PU-data based estimators for the expected risk. This allows us to develop an efficient PU random forest algorithm, PU extra trees. Our approach features three desirable properties: it is robust to the choice of the loss function in the sense that various loss functions lead to the same decision trees; it requires little hyperparameter tuning as compared to neural network based PU learning; it supports a feature importance that directly measures a feature's contribution to risk minimization. Our algorithms demonstrate strong performance on several datasets. Our code is available at \url{https://github.com/puetpaper/PUExtraTrees}.