Robust Loss Functions for Training Decision Trees with Noisy Labels
Paper and Code
Dec 20, 2023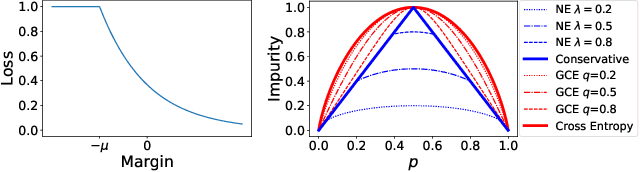


We consider training decision trees using noisily labeled data, focusing on loss functions that can lead to robust learning algorithms. Our contributions are threefold. First, we offer novel theoretical insights on the robustness of many existing loss functions in the context of decision tree learning. We show that some of the losses belong to a class of what we call conservative losses, and the conservative losses lead to an early stopping behavior during training and noise-tolerant predictions during testing. Second, we introduce a framework for constructing robust loss functions, called distribution losses. These losses apply percentile-based penalties based on an assumed margin distribution, and they naturally allow adapting to different noise rates via a robustness parameter. In particular, we introduce a new loss called the negative exponential loss, which leads to an efficient greedy impurity-reduction learning algorithm. Lastly, our experiments on multiple datasets and noise settings validate our theoretical insight and the effectiveness of our adaptive negative exponential loss.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge