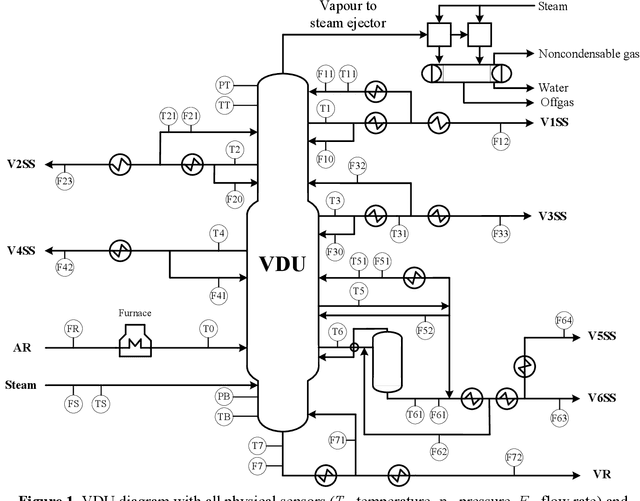
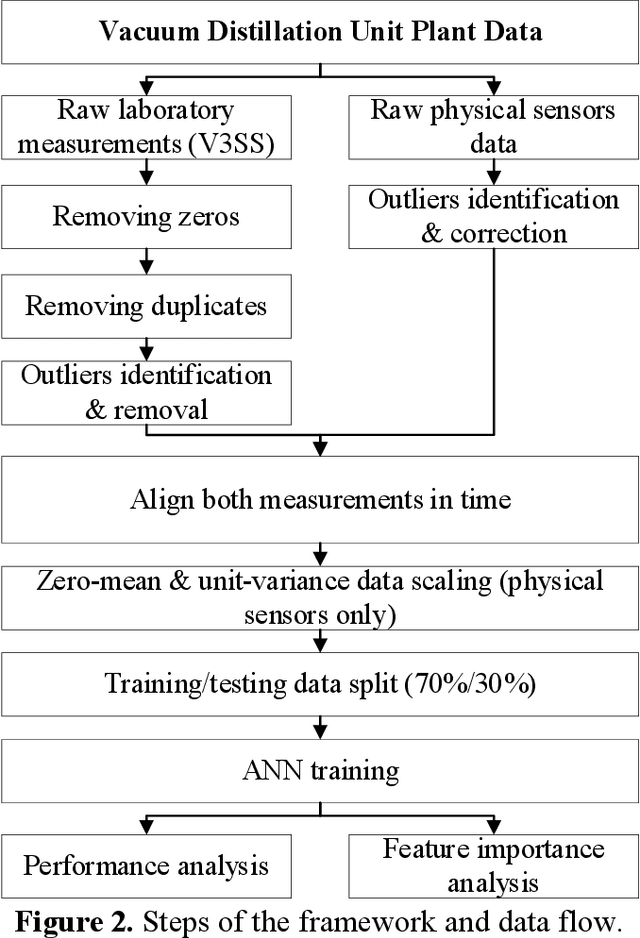
Machine Learning-Based Soft Sensors for Vacuum Distillation Unit

Product quality assessment in the petroleum processing industry can be difficult and time-consuming, e.g. due to a manual collection of liquid samples from the plant and subsequent chemical laboratory analysis of the samples. The product quality is an important property that informs whether the products of the process are within the specifications. In particular, the delays caused by sample processing (collection, laboratory measurements, results analysis, reporting) can lead to detrimental economic effects. One of the strategies to deal with this problem is soft sensors. Soft sensors are a collection of models that can be used to predict and forecast some infrequently measured properties (such as laboratory measurements of petroleum products) based on more frequent measurements of quantities like temperature, pressure and flow rate provided by physical sensors. Soft sensors short-cut the pathway to obtain relevant information about the product quality, often providing measurements as frequently as every minute. One of the applications of soft sensors is for the real-time optimization of a chemical process by a targeted adaptation of operating parameters. Models used for soft sensors can have various forms, however, among the most common are those based on artificial neural networks (ANNs). While soft sensors can deal with some of the issues in the refinery processes, their development and deployment can pose other challenges that are addressed in this paper. Firstly, it is important to enhance the quality of both sets of data (laboratory measurements and physical sensors) in a data pre-processing stage (as described in Methodology section). Secondly, once the data sets are pre-processed, different models need to be tested against prediction error and the model's interpretability. In this work, we present a framework for soft sensor development from raw data to ready-to-use models.

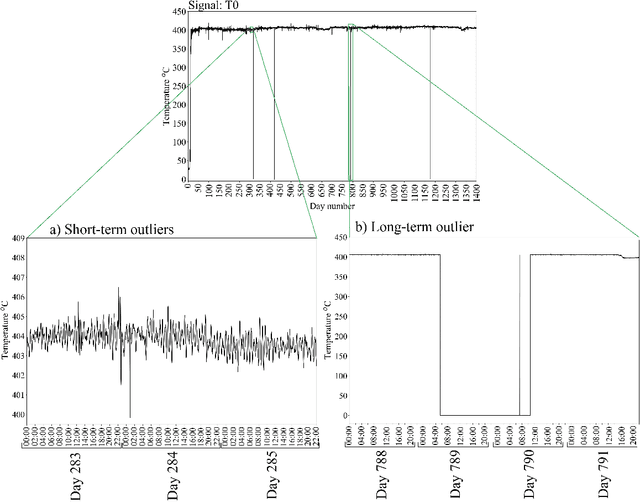
Pre-treatment of outliers and anomalies in plant data: Methodology and case study of a Vacuum Distillation Unit

Data pre-treatment plays a significant role in improving data quality, thus allowing extraction of accurate information from raw data. One of the data pre-treatment techniques commonly used is outliers detection. The so-called 3${\sigma}$ method is a common practice to identify the outliers. As shown in the manuscript, it does not identify all outliers, resulting in possible distortion of the overall statistics of the data. This problem can have a significant impact on further data analysis and can lead to reduction in the accuracy of predictive models. There is a plethora of various techniques for outliers detection, however, aside from theoretical work, they all require case study work. Two types of outliers were considered: short-term (erroneous data, noise) and long-term outliers (e.g. malfunctioning for longer periods). The data used were taken from the vacuum distillation unit (VDU) of an Asian refinery and included 40 physical sensors (temperature, pressure and flow rate). We used a modified method for 3${\sigma}$ thresholds to identify the short-term outliers, i.e. ensors data are divided into chunks determined by change points and 3${\sigma}$ thresholds are calculated within each chunk representing near-normal distribution. We have shown that piecewise 3${\sigma}$ method offers a better approach to short-term outliers detection than 3${\sigma}$ method applied to the entire time series. Nevertheless, this does not perform well for long-term outliers (which can represent another state in the data). In this case, we used principal component analysis (PCA) with Hotelling's $T^2$ statistics to identify the long-term outliers. The results obtained with PCA were subject to DBSCAN clustering method. The outliers (which were visually obvious and correctly detected by the PCA method) were also correctly identified by DBSCAN which supported the consistency and accuracy of the PCA method.

Eliminating Catastrophic Interference with Biased Competition

We present here a model to take advantage of the multi-task nature of complex datasets by learning to separate tasks and subtasks in and end to end manner by biasing competitive interactions in the network. This method does not require additional labelling or reformatting of data in a dataset. We propose an alternate view to the monolithic one-task-fits-all learning of multi-task problems, and describe a model based on a theory of neuronal attention from neuroscience, proposed by Desimone. We create and exhibit a new toy dataset, based on the MNIST dataset, which we call MNIST-QA, for testing Visual Question Answering architectures in a low-dimensional environment while preserving the more difficult components of the Visual Question Answering task, and demonstrate the proposed network architecture on this new dataset, as well as on COCO-QA and DAQUAR-FULL. We then demonstrate that this model eliminates catastrophic interference between tasks on a newly created toy dataset and provides competitive results in the Visual Question Answering space. We provide further evidence that Visual Question Answering can be approached as a multi-task problem, and demonstrate that this new architecture based on the Biased Competition model is capable of learning to separate and learn the tasks in an end-to-end fashion without the need for task labels.

Visual Question Answering as a Multi-Task Problem

Visual Question Answering(VQA) is a highly complex problem set, relying on many sub-problems to produce reasonable answers. In this paper, we present the hypothesis that Visual Question Answering should be viewed as a multi-task problem, and provide evidence to support this hypothesis. We demonstrate this by reformatting two commonly used Visual Question Answering datasets, COCO-QA and DAQUAR, into a multi-task format and train these reformatted datasets on two baseline networks, with one designed specifically to eliminate other possible causes for performance changes as a result of the reformatting. Though the networks demonstrated in this paper do not achieve strongly competitive results, we find that the multi-task approach to Visual Question Answering results in increases in performance of 5-9% against the single-task formatting, and that the networks reach convergence much faster than in the single-task case. Finally we discuss possible reasons for the observed difference in performance, and perform additional experiments which rule out causes not associated with the learning of the dataset as a multi-task problem.