A Continuous Max-Flow Approach to Cyclic Field Reconstruction

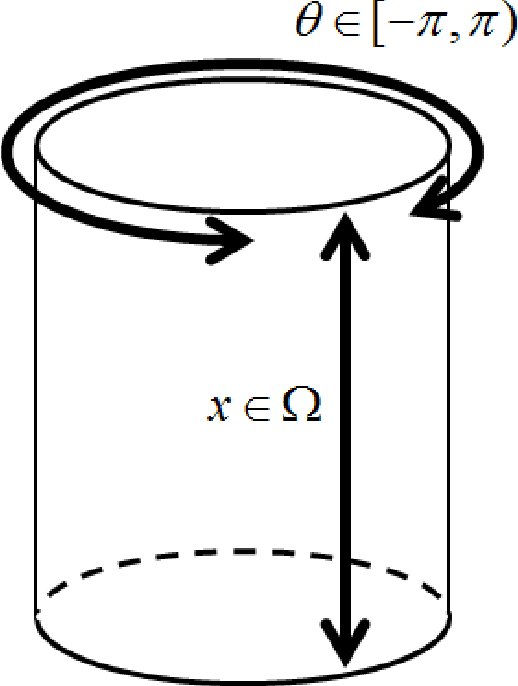
Reconstruction of an image from noisy data using Markov Random Field theory has been explored by both the graph-cuts and continuous max-flow community in the form of the Potts and Ishikawa models. However, neither model takes into account the particular cyclic topology of specific intensity types such as the hue in natural colour images, or the phase in complex valued MRI. This paper presents \textit{cyclic continuous max-flow} image reconstruction which models the intensity being reconstructed as having a fundamentally cyclic topology. This model complements the Ishikawa model in that it is designed with image reconstruction in mind, having the topology of the intensity space inherent in the model while being readily extendable to an arbitrary intensity resolution.

Shape Complexes in Continuous Max-Flow Hierarchical Multi-Labeling Problems

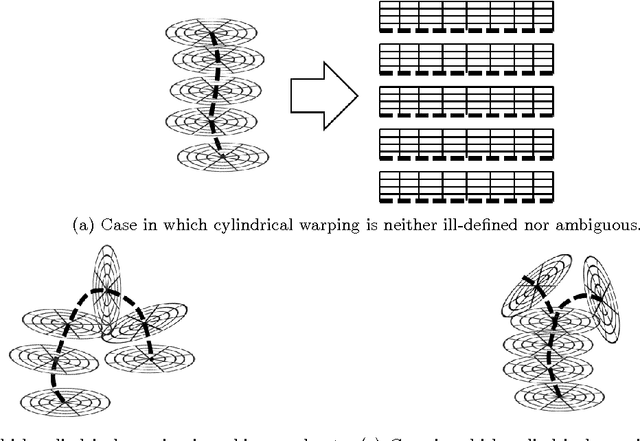
Although topological considerations amongst multiple labels have been previously investigated in the context of continuous max-flow image segmentation, similar investigations have yet to be made about shape considerations in a general and extendable manner. This paper presents shape complexes for segmentation, which capture more complex shapes by combining multiple labels and super-labels constrained by geodesic star convexity. Shape complexes combine geodesic star convexity constraints with hierarchical label organization, which together allow for more complex shapes to be represented. This framework avoids the use of co-ordinate system warping techniques to convert shape constraints into topological constraints, which may be ambiguous or ill-defined for certain segmentation problems.

A Proximal Bregman Projection Approach to Continuous Max-Flow Problems Using Entropic Distances

One issue limiting the adaption of large-scale multi-region segmentation is the sometimes prohibitive memory requirements. This is especially troubling considering advances in massively parallel computing and commercial graphics processing units because of their already limited memory compared to the current random access memory used in more traditional computation. To address this issue in the field of continuous max-flow segmentation, we have developed a \textit{pseudo-flow} framework using the theory of Bregman proximal projections and entropic distances which implicitly represents flow variables between labels and designated source and sink nodes. This reduces the memory requirements for max-flow segmentation by approximately 20\% for Potts models and approximately 30\% for hierarchical max-flow (HMF) and directed acyclic graph max-flow (DAGMF) models. This represents a great improvement in the state-of-the-art in max-flow segmentation, allowing for much larger problems to be addressed and accelerated using commercially available graphics processing hardware.

A Continuous Max-Flow Approach to Multi-Labeling Problems under Arbitrary Region Regularization

The incorporation of region regularization into max-flow segmentation has traditionally focused on ordering and part-whole relationships. A side effect of the development of such models is that it constrained regularization only to those cases, rather than allowing for arbitrary region regularization. Directed Acyclic Graphical Max-Flow (DAGMF) segmentation overcomes these limitations by allowing for the algorithm designer to specify an arbitrary directed acyclic graph to structure a max-flow segmentation. This allows for individual 'parts' to be a member of multiple distinct 'wholes.'

A Continuous Max-Flow Approach to General Hierarchical Multi-Labeling Problems

Multi-region segmentation algorithms often have the onus of incorporating complex anatomical knowledge representing spatial or geometric relationships between objects, and general-purpose methods of addressing this knowledge in an optimization-based manner have thus been lacking. This paper presents Generalized Hierarchical Max-Flow (GHMF) segmentation, which captures simple anatomical part-whole relationships in the form of an unconstrained hierarchy. Regularization can then be applied to both parts and wholes independently, allowing for spatial grouping and clustering of labels in a globally optimal convex optimization framework. For the purposes of ready integration into a variety of segmentation tasks, the hierarchies can be presented in run-time, allowing for the segmentation problem to be readily specified and alternatives explored without undue programming effort or recompilation.

RANCOR: Non-Linear Image Registration with Total Variation Regularization

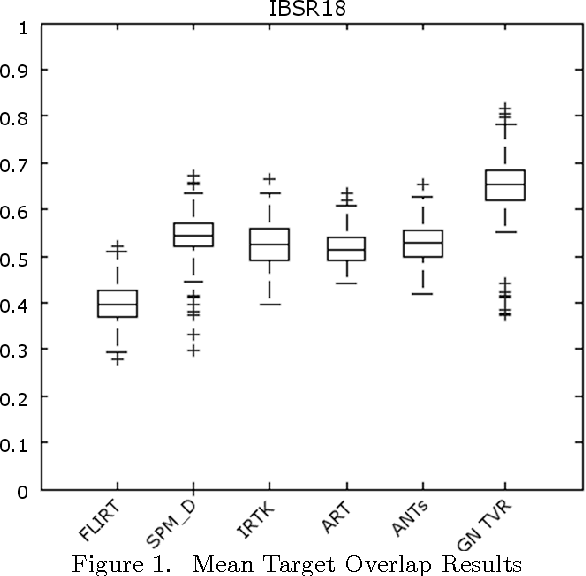
Optimization techniques have been widely used in deformable registration, allowing for the incorporation of similarity metrics with regularization mechanisms. These regularization mechanisms are designed to mitigate the effects of trivial solutions to ill-posed registration problems and to otherwise ensure the resulting deformation fields are well-behaved. This paper introduces a novel deformable registration algorithm, RANCOR, which uses iterative convexification to address deformable registration problems under total-variation regularization. Initial comparative results against four state-of-the-art registration algorithms are presented using the Internet Brain Segmentation Repository (IBSR) database.