A Continuous Max-Flow Approach to Cyclic Field Reconstruction
Paper and Code
Nov 11, 2015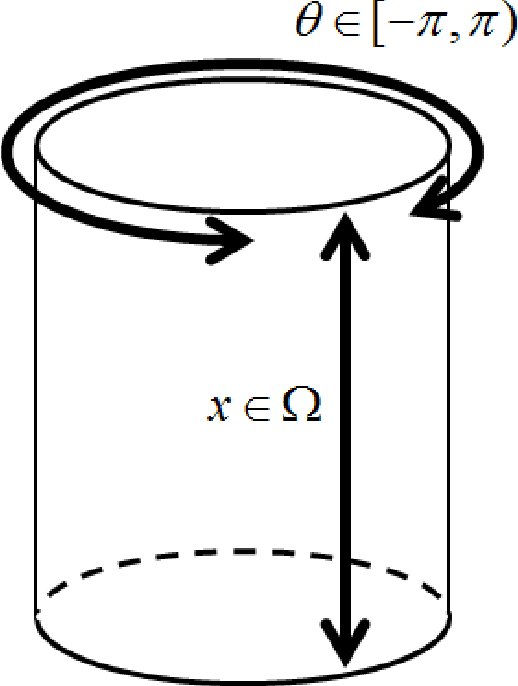
Reconstruction of an image from noisy data using Markov Random Field theory has been explored by both the graph-cuts and continuous max-flow community in the form of the Potts and Ishikawa models. However, neither model takes into account the particular cyclic topology of specific intensity types such as the hue in natural colour images, or the phase in complex valued MRI. This paper presents \textit{cyclic continuous max-flow} image reconstruction which models the intensity being reconstructed as having a fundamentally cyclic topology. This model complements the Ishikawa model in that it is designed with image reconstruction in mind, having the topology of the intensity space inherent in the model while being readily extendable to an arbitrary intensity resolution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge