A Unifying Theory of Thompson Sampling for Continuous Risk-Averse Bandits

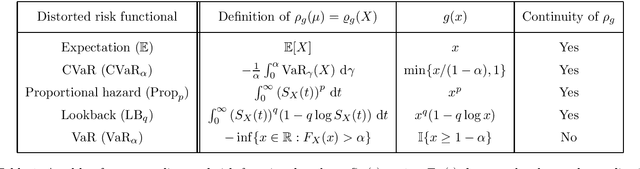
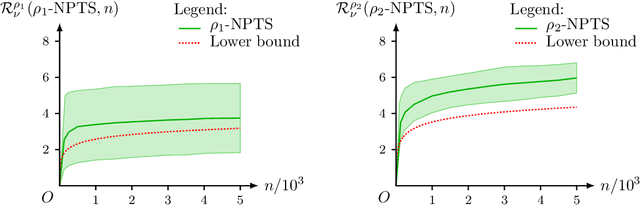
This paper unifies the design and simplifies the analysis of risk-averse Thompson sampling algorithms for the multi-armed bandit problem for a generic class of risk functionals \r{ho} that are continuous. Using the contraction principle in the theory of large deviations, we prove novel concentration bounds for these continuous risk functionals. In contrast to existing works in which the bounds depend on the samples themselves, our bounds only depend on the number of samples. This allows us to sidestep significant analytical challenges and unify existing proofs of the regret bounds of existing Thompson sampling-based algorithms. We show that a wide class of risk functionals as well as "nice" functions of them satisfy the continuity condition. Using our newly developed analytical toolkits, we analyse the algorithms $\rho$-MTS (for multinomial distributions) and $\rho$-NPTS (for bounded distributions) and prove that they admit asymptotically optimal regret bounds of risk-averse algorithms under the mean-variance, CVaR, and other ubiquitous risk measures, as well as a host of newly synthesized risk measures. Numerical simulations show that our bounds are reasonably tight vis-\`a-vis algorithm-independent lower bounds.

Thompson Sampling for Gaussian Entropic Risk Bandits

The multi-armed bandit (MAB) problem is a ubiquitous decision-making problem that exemplifies exploration-exploitation tradeoff. Standard formulations exclude risk in decision making. Risknotably complicates the basic reward-maximising objectives, in part because there is no universally agreed definition of it. In this paper, we consider an entropic risk (ER) measure and explore the performance of a Thompson sampling-based algorithm ERTS under this risk measure by providing regret bounds for ERTS and corresponding instance dependent lower bounds.

Risk-Constrained Thompson Sampling for CVaR Bandits

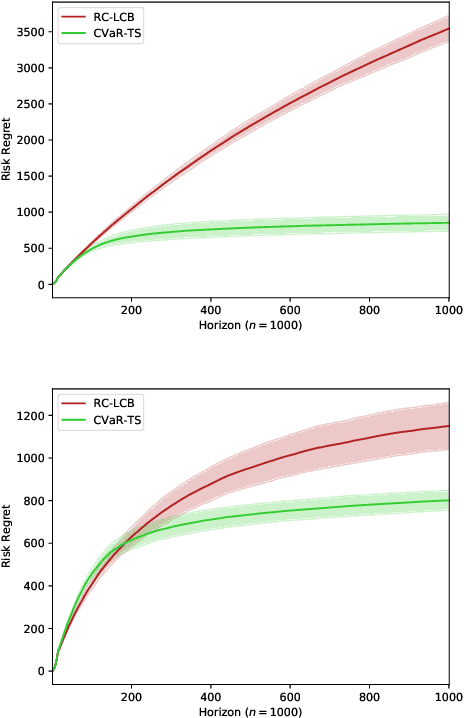
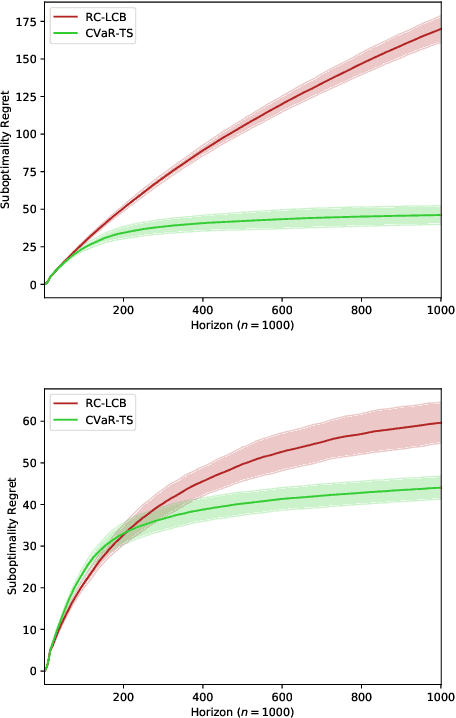
The multi-armed bandit (MAB) problem is a ubiquitous decision-making problem that exemplifies the exploration-exploitation tradeoff. Standard formulations exclude risk in decision making. Risk notably complicates the basic reward-maximising objective, in part because there is no universally agreed definition of it. In this paper, we consider a popular risk measure in quantitative finance known as the Conditional Value at Risk (CVaR). We explore the performance of a Thompson Sampling-based algorithm CVaR-TS under this risk measure. We provide comprehensive comparisons between our regret bounds with state-of-the-art L/UCB-based algorithms in comparable settings and demonstrate their clear improvement in performance. We also include numerical simulations to empirically verify that CVaR-TS outperforms other L/UCB-based algorithms.