A Unifying Theory of Thompson Sampling for Continuous Risk-Averse Bandits

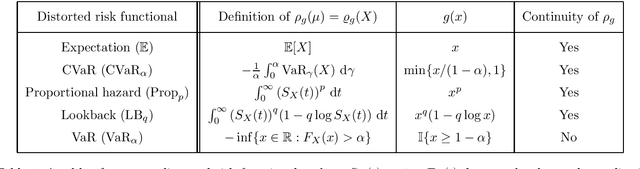
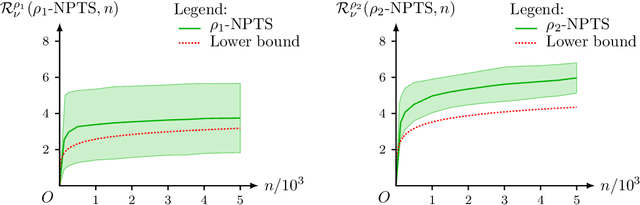
This paper unifies the design and simplifies the analysis of risk-averse Thompson sampling algorithms for the multi-armed bandit problem for a generic class of risk functionals \r{ho} that are continuous. Using the contraction principle in the theory of large deviations, we prove novel concentration bounds for these continuous risk functionals. In contrast to existing works in which the bounds depend on the samples themselves, our bounds only depend on the number of samples. This allows us to sidestep significant analytical challenges and unify existing proofs of the regret bounds of existing Thompson sampling-based algorithms. We show that a wide class of risk functionals as well as "nice" functions of them satisfy the continuity condition. Using our newly developed analytical toolkits, we analyse the algorithms $\rho$-MTS (for multinomial distributions) and $\rho$-NPTS (for bounded distributions) and prove that they admit asymptotically optimal regret bounds of risk-averse algorithms under the mean-variance, CVaR, and other ubiquitous risk measures, as well as a host of newly synthesized risk measures. Numerical simulations show that our bounds are reasonably tight vis-\`a-vis algorithm-independent lower bounds.