Weakly-Supervised Deep Learning of Heat Transport via Physics Informed Loss

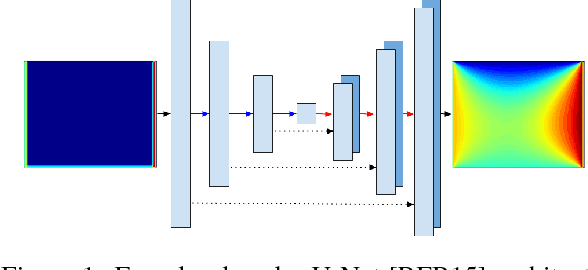
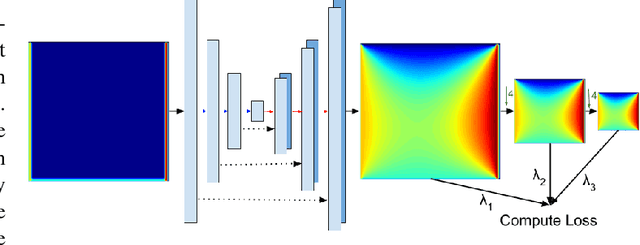
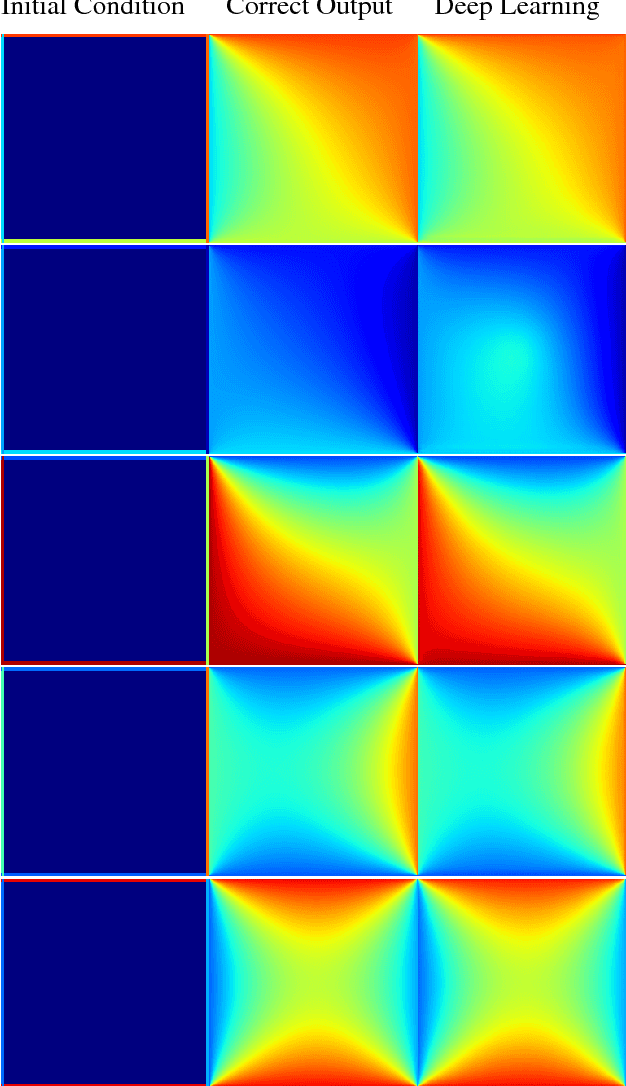
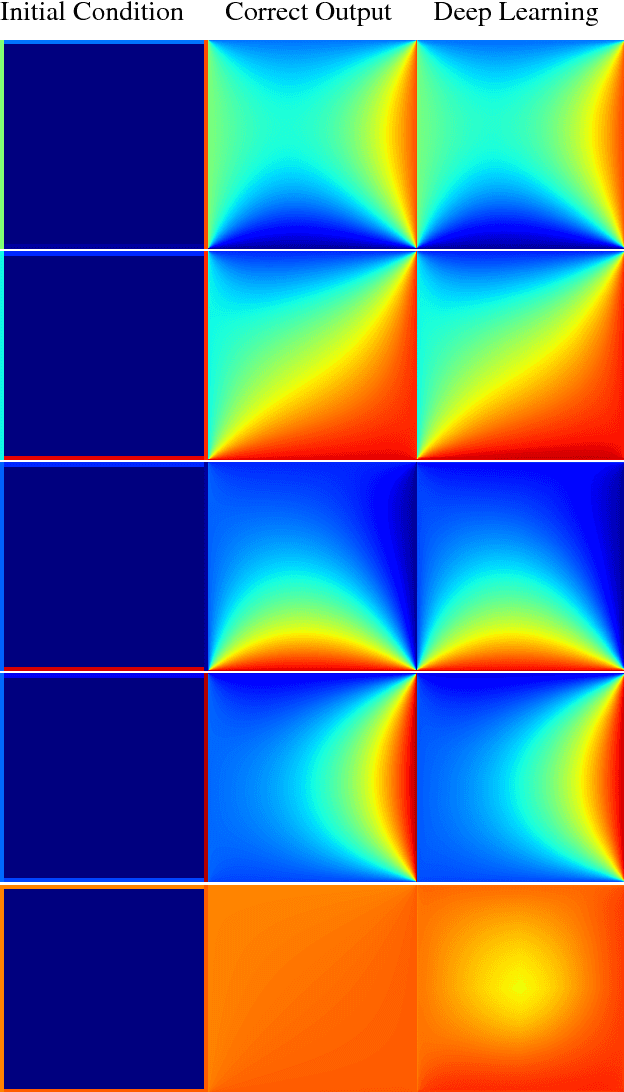
In typical machine learning tasks and applications, it is necessary to obtain or create large labeled datasets in order to to achieve high performance. Unfortunately, large labeled datasets are not always available and can be expensive to source, creating a bottleneck towards more widely applicable machine learning. The paradigm of weak supervision offers an alternative that allows for integration of domain-specific knowledge by enforcing constraints that a correct solution to the learning problem will obey over the output space. In this work, we explore the application of this paradigm to 2-D physical systems governed by non-linear differential equations. We demonstrate that knowledge of the partial differential equations governing a system can be encoded into the loss function of a neural network via an appropriately chosen convolutional kernel. We demonstrate this by showing that the steady-state solution to the 2-D heat equation can be learned directly from initial conditions by a convolutional neural network, in the absence of labeled training data. We also extend recent work in the progressive growing of fully convolutional networks to achieve high accuracy (< 1.5% error) at multiple scales of the heat-flow problem, including at the very large scale (1024x1024). Finally, we demonstrate that this method can be used to speed up exact calculation of the solution to the differential equations via finite difference.