Formal Explanations for Neuro-Symbolic AI

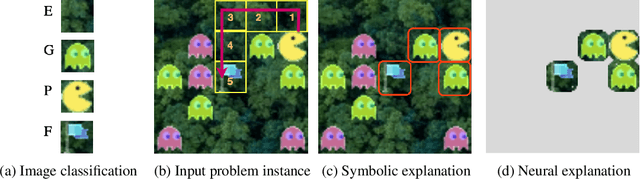
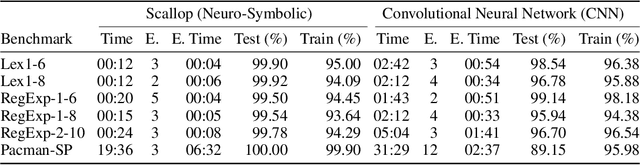
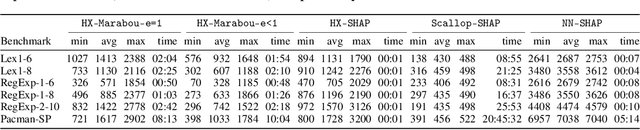
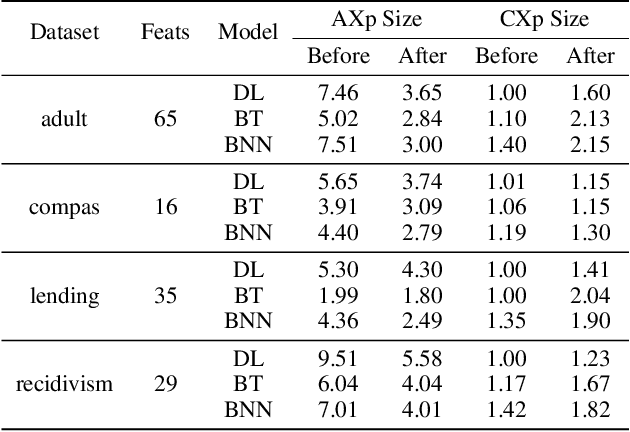
Despite the practical success of Artificial Intelligence (AI), current neural AI algorithms face two significant issues. First, the decisions made by neural architectures are often prone to bias and brittleness. Second, when a chain of reasoning is required, neural systems often perform poorly. Neuro-symbolic artificial intelligence is a promising approach that tackles these (and other) weaknesses by combining the power of neural perception and symbolic reasoning. Meanwhile, the success of AI has made it critical to understand its behaviour, leading to the development of explainable artificial intelligence (XAI). While neuro-symbolic AI systems have important advantages over purely neural AI, we still need to explain their actions, which are obscured by the interactions of the neural and symbolic components. To address the issue, this paper proposes a formal approach to explaining the decisions of neuro-symbolic systems. The approach hinges on the use of formal abductive explanations and on solving the neuro-symbolic explainability problem hierarchically. Namely, it first computes a formal explanation for the symbolic component of the system, which serves to identify a subset of the individual parts of neural information that needs to be explained. This is followed by explaining only those individual neural inputs, independently of each other, which facilitates succinctness of hierarchical formal explanations and helps to increase the overall performance of the approach. Experimental results for a few complex reasoning tasks demonstrate practical efficiency of the proposed approach, in comparison to purely neural systems, from the perspective of explanation size, explanation time, training time, model sizes, and the quality of explanations reported.

Anytime Approximate Formal Feature Attribution

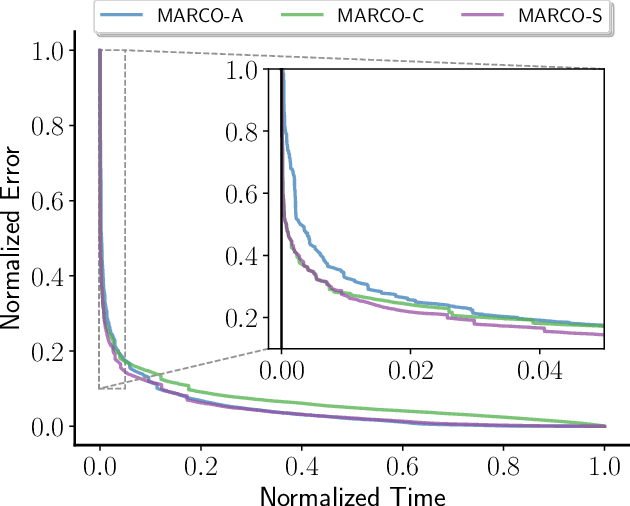
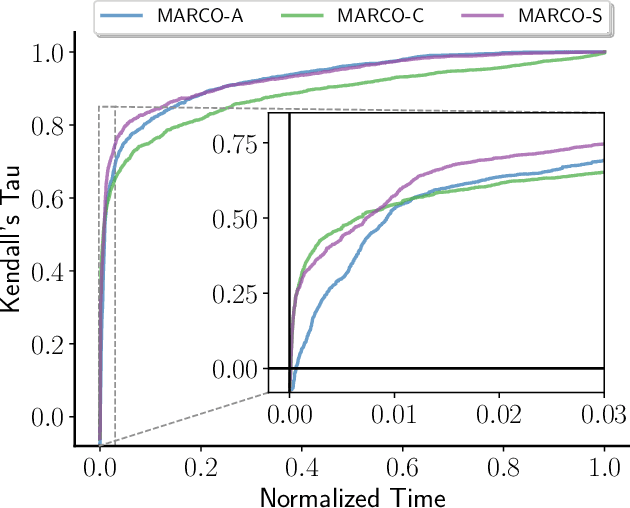
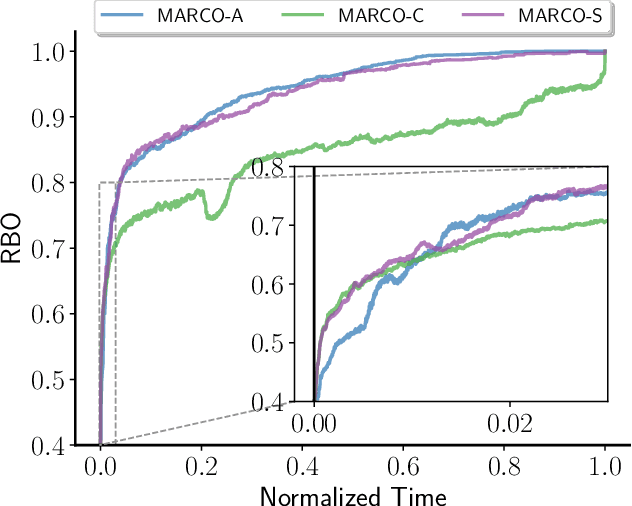
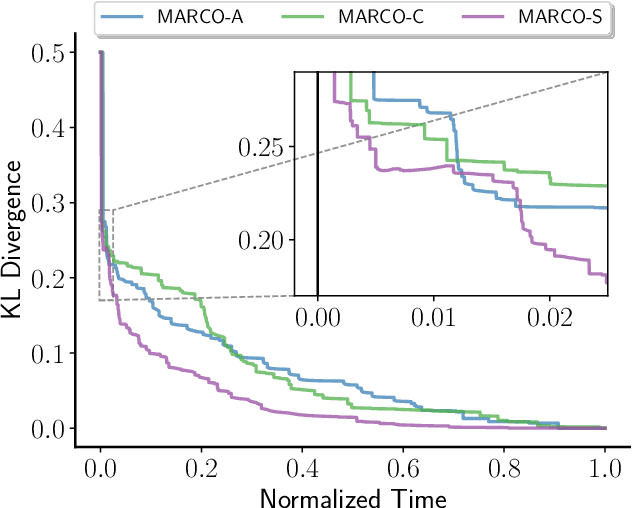
Widespread use of artificial intelligence (AI) algorithms and machine learning (ML) models on the one hand and a number of crucial issues pertaining to them warrant the need for explainable artificial intelligence (XAI). A key explainability question is: given this decision was made, what are the input features which contributed to the decision? Although a range of XAI approaches exist to tackle this problem, most of them have significant limitations. Heuristic XAI approaches suffer from the lack of quality guarantees, and often try to approximate Shapley values, which is not the same as explaining which features contribute to a decision. A recent alternative is so-called formal feature attribution (FFA), which defines feature importance as the fraction of formal abductive explanations (AXp's) containing the given feature. This measures feature importance from the view of formally reasoning about the model's behavior. It is challenging to compute FFA using its definition because that involves counting AXp's, although one can approximate it. Based on these results, this paper makes several contributions. First, it gives compelling evidence that computing FFA is intractable, even if the set of contrastive formal explanations (CXp's) is provided, by proving that the problem is #P-hard. Second, by using the duality between AXp's and CXp's, it proposes an efficient heuristic to switch from CXp enumeration to AXp enumeration on-the-fly resulting in an adaptive explanation enumeration algorithm effectively approximating FFA in an anytime fashion. Finally, experimental results obtained on a range of widely used datasets demonstrate the effectiveness of the proposed FFA approximation approach in terms of the error of FFA approximation as well as the number of explanations computed and their diversity given a fixed time limit.

On Formal Feature Attribution and Its Approximation

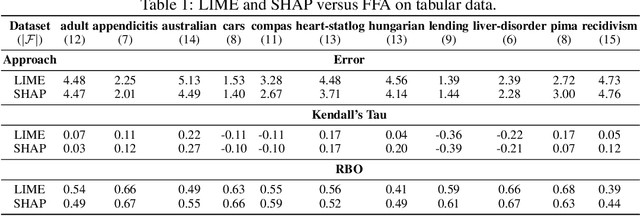
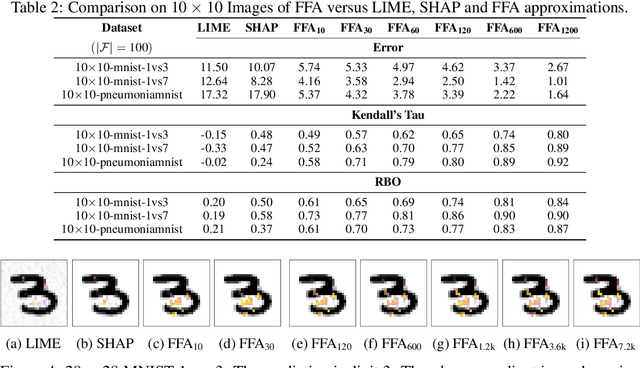
Recent years have witnessed the widespread use of artificial intelligence (AI) algorithms and machine learning (ML) models. Despite their tremendous success, a number of vital problems like ML model brittleness, their fairness, and the lack of interpretability warrant the need for the active developments in explainable artificial intelligence (XAI) and formal ML model verification. The two major lines of work in XAI include feature selection methods, e.g. Anchors, and feature attribution techniques, e.g. LIME and SHAP. Despite their promise, most of the existing feature selection and attribution approaches are susceptible to a range of critical issues, including explanation unsoundness and out-of-distribution sampling. A recent formal approach to XAI (FXAI) although serving as an alternative to the above and free of these issues suffers from a few other limitations. For instance and besides the scalability limitation, the formal approach is unable to tackle the feature attribution problem. Additionally, a formal explanation despite being formally sound is typically quite large, which hampers its applicability in practical settings. Motivated by the above, this paper proposes a way to apply the apparatus of formal XAI to the case of feature attribution based on formal explanation enumeration. Formal feature attribution (FFA) is argued to be advantageous over the existing methods, both formal and non-formal. Given the practical complexity of the problem, the paper then proposes an efficient technique for approximating exact FFA. Finally, it offers experimental evidence of the effectiveness of the proposed approximate FFA in comparison to the existing feature attribution algorithms not only in terms of feature importance and but also in terms of their relative order.

Eliminating The Impossible, Whatever Remains Must Be True

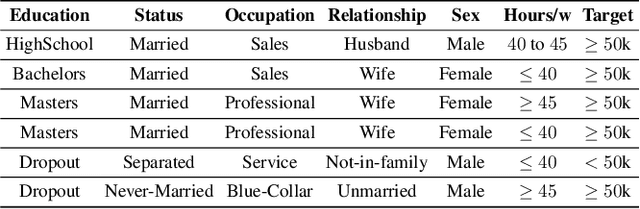
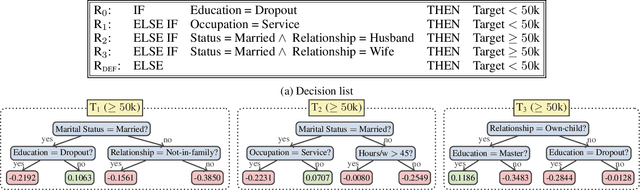
The rise of AI methods to make predictions and decisions has led to a pressing need for more explainable artificial intelligence (XAI) methods. One common approach for XAI is to produce a post-hoc explanation, explaining why a black box ML model made a certain prediction. Formal approaches to post-hoc explanations provide succinct reasons for why a prediction was made, as well as why not another prediction was made. But these approaches assume that features are independent and uniformly distributed. While this means that "why" explanations are correct, they may be longer than required. It also means the "why not" explanations may be suspect as the counterexamples they rely on may not be meaningful. In this paper, we show how one can apply background knowledge to give more succinct "why" formal explanations, that are presumably easier to interpret by humans, and give more accurate "why not" explanations. Furthermore, we also show how to use existing rule induction techniques to efficiently extract background information from a dataset, and also how to report which background information was used to make an explanation, allowing a human to examine it if they doubt the correctness of the explanation.

Optimal Decision Lists using SAT

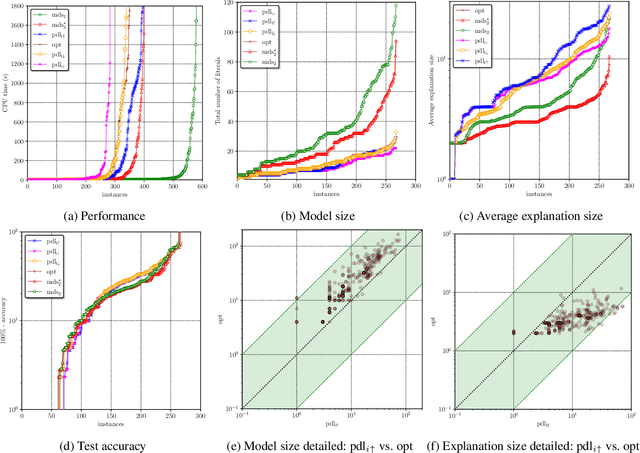
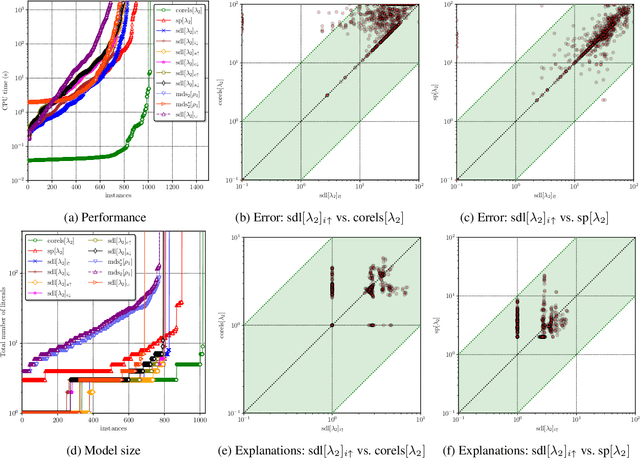
Decision lists are one of the most easily explainable machine learning models. Given the renewed emphasis on explainable machine learning decisions, this machine learning model is increasingly attractive, combining small size and clear explainability. In this paper, we show for the first time how to construct optimal "perfect" decision lists which are perfectly accurate on the training data, and minimal in size, making use of modern SAT solving technology. We also give a new method for determining optimal sparse decision lists, which trade off size and accuracy. We contrast the size and test accuracy of optimal decisions lists versus optimal decision sets, as well as other state-of-the-art methods for determining optimal decision lists. We also examine the size of average explanations generated by decision sets and decision lists.

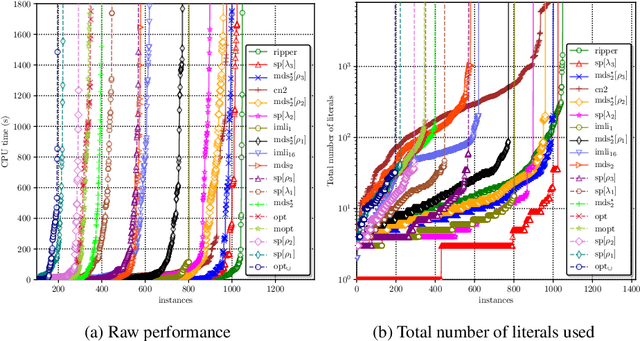
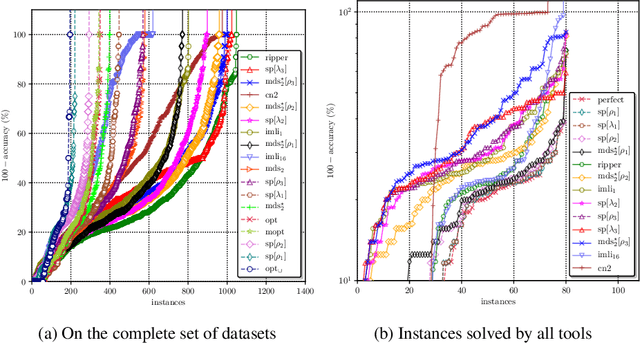
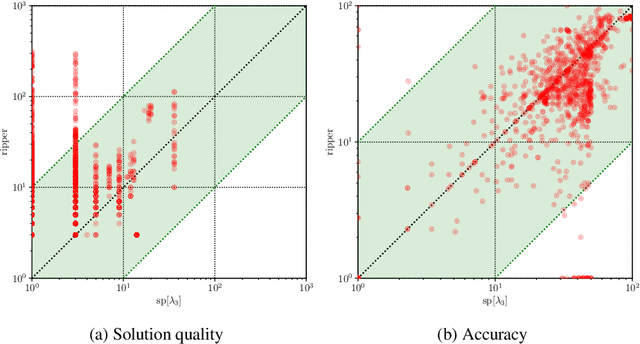
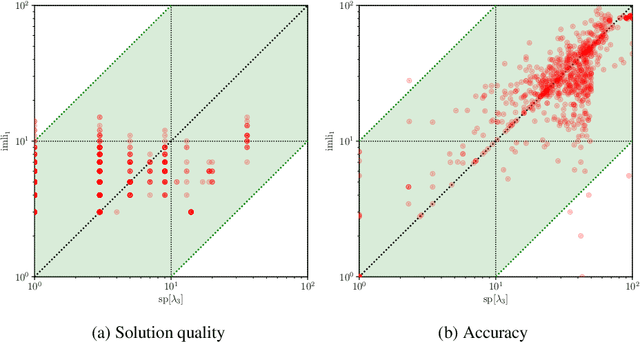
Computing Optimal Decision Sets with SAT

As machine learning is increasingly used to help make decisions, there is a demand for these decisions to be explainable. Arguably, the most explainable machine learning models use decision rules. This paper focuses on decision sets, a type of model with unordered rules, which explains each prediction with a single rule. In order to be easy for humans to understand, these rules must be concise. Earlier work on generating optimal decision sets first minimizes the number of rules, and then minimizes the number of literals, but the resulting rules can often be very large. Here we consider a better measure, namely the total size of the decision set in terms of literals. So we are not driven to a small set of rules which require a large number of literals. We provide the first approach to determine minimum-size decision sets that achieve minimum empirical risk and then investigate sparse alternatives where we trade accuracy for size. By finding optimal solutions we show we can build decision set classifiers that are almost as accurate as the best heuristic methods, but far more concise, and hence more explainable.