Domain Adaptation-based Edge Computing for Cross-Conditions Fault Diagnosis

Fault diagnosis technology supports the healthy operation of mechanical equipment. However, the variations conditions during the operation of mechanical equipment lead to significant disparities in data distribution, posing challenges to fault diagnosis. Furthermore, when deploying applications, traditional methods often encounter issues such as latency and data security. Therefore, conducting fault diagnosis and deploying application methods under cross-operating conditions holds significant value. This paper proposes a domain adaptation-based lightweight fault diagnosis framework for edge computing scenarios. Incorporating the local maximum mean discrepancy into knowledge transfer aligns the feature distributions of different domains in a high-dimensional feature space, to discover a common feature space across domains. The acquired fault diagnosis expertise from the cloud-model is transferred to the lightweight edge-model using adaptation knowledge transfer methods. While ensuring real-time diagnostic capabilities, accurate fault diagnosis is achieved across working conditions. We conducted validation experiments on the NVIDIA Jetson Xavier NX kit. In terms of diagnostic performance, the proposed method significantly improved diagnostic accuracy, with average increases of 34.44% and 17.33% compared to the comparison method, respectively. Regarding lightweight effectiveness, proposed method achieved an average inference speed increase of 80.47%. Additionally, compared to the cloud-model, the parameter count of the edge-model decreased by 96.37%, while the Flops decreased by 83.08%.

Dynamic Gaussian Graph Operator: Learning parametric partial differential equations in arbitrary discrete mechanics problems

Deep learning methods have access to be employed for solving physical systems governed by parametric partial differential equations (PDEs) due to massive scientific data. It has been refined to operator learning that focuses on learning non-linear mapping between infinite-dimensional function spaces, offering interface from observations to solutions. However, state-of-the-art neural operators are limited to constant and uniform discretization, thereby leading to deficiency in generalization on arbitrary discretization schemes for computational domain. In this work, we propose a novel operator learning algorithm, referred to as Dynamic Gaussian Graph Operator (DGGO) that expands neural operators to learning parametric PDEs in arbitrary discrete mechanics problems. The Dynamic Gaussian Graph (DGG) kernel learns to map the observation vectors defined in general Euclidean space to metric vectors defined in high-dimensional uniform metric space. The DGG integral kernel is parameterized by Gaussian kernel weighted Riemann sum approximating and using dynamic message passing graph to depict the interrelation within the integral term. Fourier Neural Operator is selected to localize the metric vectors on spatial and frequency domains. Metric vectors are regarded as located on latent uniform domain, wherein spatial and spectral transformation offer highly regular constraints on solution space. The efficiency and robustness of DGGO are validated by applying it to solve numerical arbitrary discrete mechanics problems in comparison with mainstream neural operators. Ablation experiments are implemented to demonstrate the effectiveness of spatial transformation in the DGG kernel. The proposed method is utilized to forecast stress field of hyper-elastic material with geometrically variable void as engineering application.

MPIPN: A Multi Physics-Informed PointNet for solving parametric acoustic-structure systems

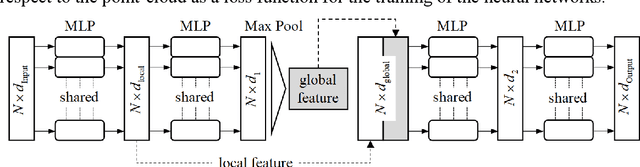
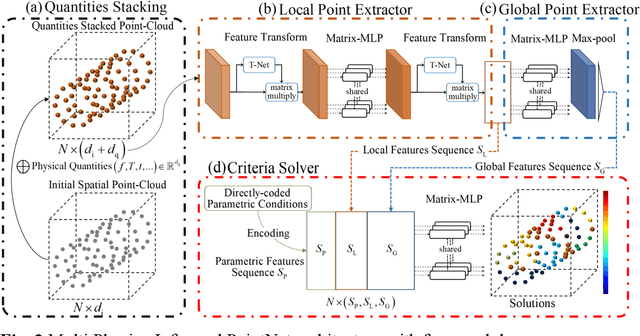
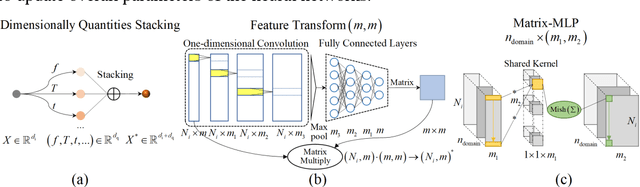
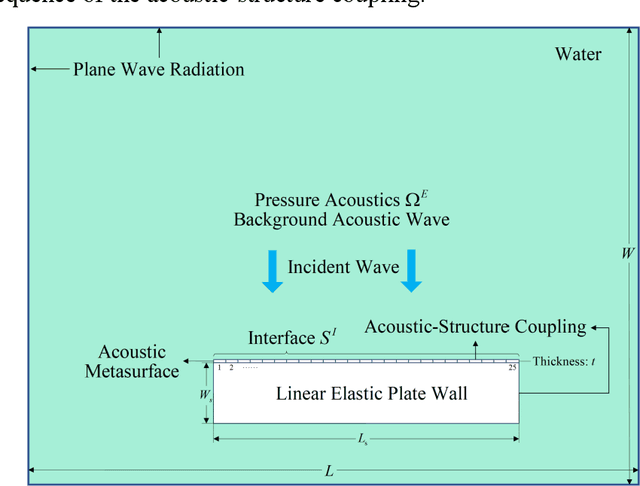
Machine learning is employed for solving physical systems governed by general nonlinear partial differential equations (PDEs). However, complex multi-physics systems such as acoustic-structure coupling are often described by a series of PDEs that incorporate variable physical quantities, which are referred to as parametric systems. There are lack of strategies for solving parametric systems governed by PDEs that involve explicit and implicit quantities. In this paper, a deep learning-based Multi Physics-Informed PointNet (MPIPN) is proposed for solving parametric acoustic-structure systems. First, the MPIPN induces an enhanced point-cloud architecture that encompasses explicit physical quantities and geometric features of computational domains. Then, the MPIPN extracts local and global features of the reconstructed point-cloud as parts of solving criteria of parametric systems, respectively. Besides, implicit physical quantities are embedded by encoding techniques as another part of solving criteria. Finally, all solving criteria that characterize parametric systems are amalgamated to form distinctive sequences as the input of the MPIPN, whose outputs are solutions of systems. The proposed framework is trained by adaptive physics-informed loss functions for corresponding computational domains. The framework is generalized to deal with new parametric conditions of systems. The effectiveness of the MPIPN is validated by applying it to solve steady parametric acoustic-structure coupling systems governed by the Helmholtz equations. An ablation experiment has been implemented to demonstrate the efficacy of physics-informed impact with a minority of supervised data. The proposed method yields reasonable precision across all computational domains under constant parametric conditions and changeable combinations of parametric conditions for acoustic-structure systems.