Jingxuan Chai
Rate-Distortion-Perception Theory for Semantic Communication
Dec 09, 2023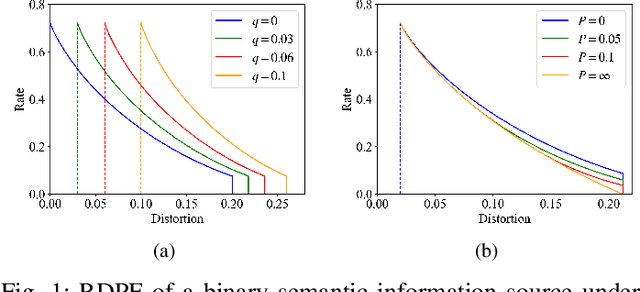
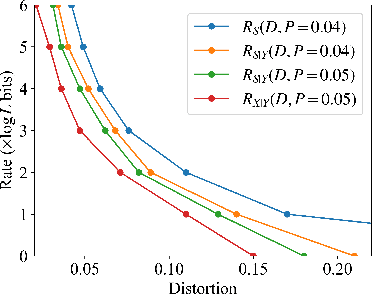
Abstract:Semantic communication has attracted significant interest recently due to its capability to meet the fast growing demand on user-defined and human-oriented communication services such as holographic communications, eXtended reality (XR), and human-to-machine interactions. Unfortunately, recent study suggests that the traditional Shannon information theory, focusing mainly on delivering semantic-agnostic symbols, will not be sufficient to investigate the semantic-level perceptual quality of the recovered messages at the receiver. In this paper, we study the achievable data rate of semantic communication under the symbol distortion and semantic perception constraints. Motivated by the fact that the semantic information generally involves rich intrinsic knowledge that cannot always be directly observed by the encoder, we consider a semantic information source that can only be indirectly sensed by the encoder. Both encoder and decoder can access to various types of side information that may be closely related to the user's communication preference. We derive the achievable region that characterizes the tradeoff among the data rate, symbol distortion, and semantic perception, which is then theoretically proved to be achievable by a stochastic coding scheme. We derive a closed-form achievable rate for binary semantic information source under any given distortion and perception constraints. We observe that there exists cases that the receiver can directly infer the semantic information source satisfying certain distortion and perception constraints without requiring any data communication from the transmitter. Experimental results based on the image semantic source signal have been presented to verify our theoretical observations.
ModulE: Module Embedding for Knowledge Graphs
Mar 09, 2022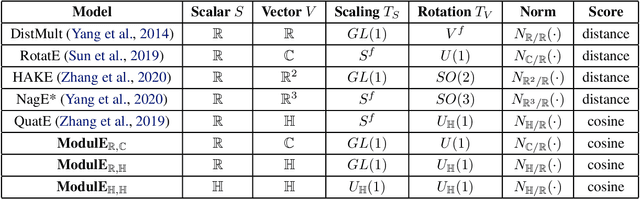
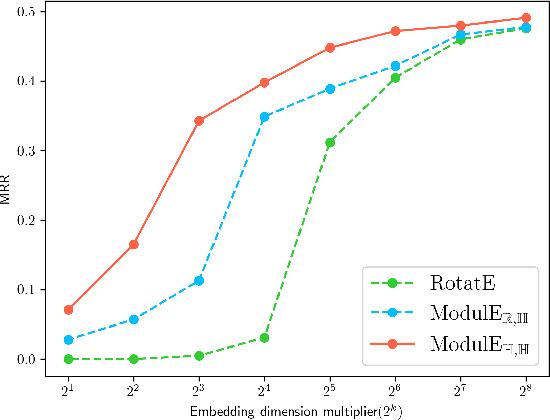
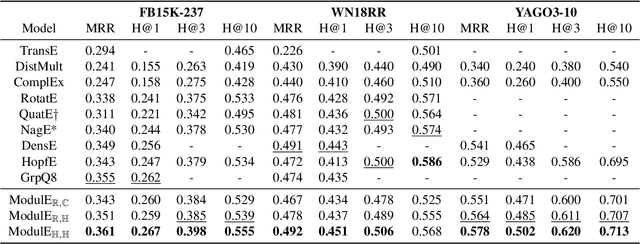
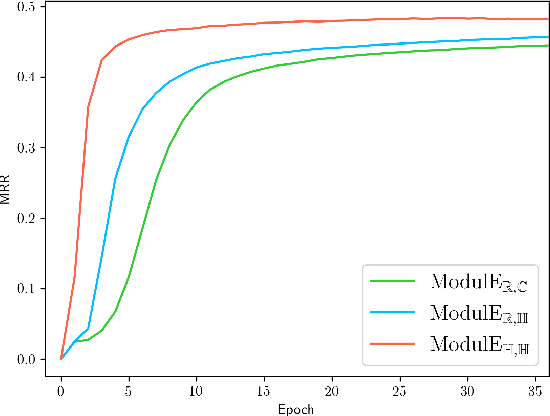
Abstract:Knowledge graph embedding (KGE) has been shown to be a powerful tool for predicting missing links of a knowledge graph. However, existing methods mainly focus on modeling relation patterns, while simply embed entities to vector spaces, such as real field, complex field and quaternion space. To model the embedding space from a more rigorous and theoretical perspective, we propose a novel general group theory-based embedding framework for rotation-based models, in which both entities and relations are embedded as group elements. Furthermore, in order to explore more available KGE models, we utilize a more generic group structure, module, a generalization notion of vector space. Specifically, under our framework, we introduce a more generic embedding method, ModulE, which projects entities to a module. Following the method of ModulE, we build three instantiating models: ModulE$_{\mathbb{R},\mathbb{C}}$, ModulE$_{\mathbb{R},\mathbb{H}}$ and ModulE$_{\mathbb{H},\mathbb{H}}$, by adopting different module structures. Experimental results show that ModulE$_{\mathbb{H},\mathbb{H}}$ which embeds entities to a module over non-commutative ring, achieves state-of-the-art performance on multiple benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge