ModulE: Module Embedding for Knowledge Graphs
Paper and Code
Mar 09, 2022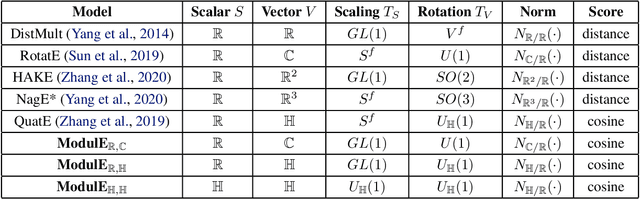
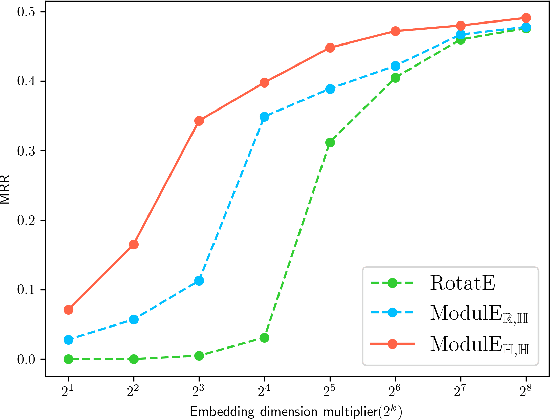
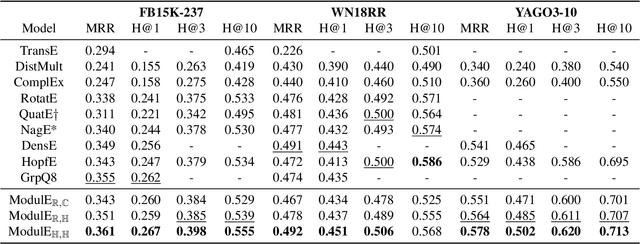
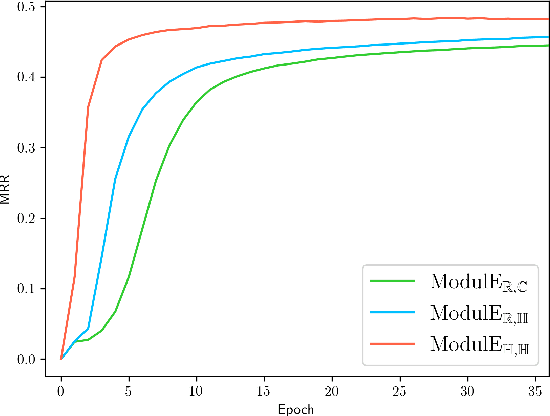
Knowledge graph embedding (KGE) has been shown to be a powerful tool for predicting missing links of a knowledge graph. However, existing methods mainly focus on modeling relation patterns, while simply embed entities to vector spaces, such as real field, complex field and quaternion space. To model the embedding space from a more rigorous and theoretical perspective, we propose a novel general group theory-based embedding framework for rotation-based models, in which both entities and relations are embedded as group elements. Furthermore, in order to explore more available KGE models, we utilize a more generic group structure, module, a generalization notion of vector space. Specifically, under our framework, we introduce a more generic embedding method, ModulE, which projects entities to a module. Following the method of ModulE, we build three instantiating models: ModulE$_{\mathbb{R},\mathbb{C}}$, ModulE$_{\mathbb{R},\mathbb{H}}$ and ModulE$_{\mathbb{H},\mathbb{H}}$, by adopting different module structures. Experimental results show that ModulE$_{\mathbb{H},\mathbb{H}}$ which embeds entities to a module over non-commutative ring, achieves state-of-the-art performance on multiple benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge