Consistency of Neural Networks with Regularization

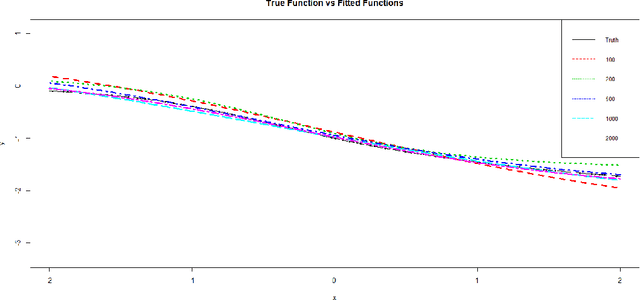
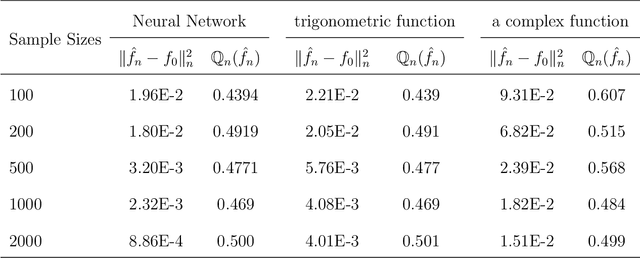
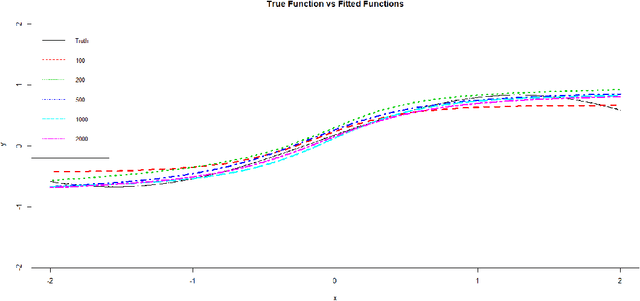
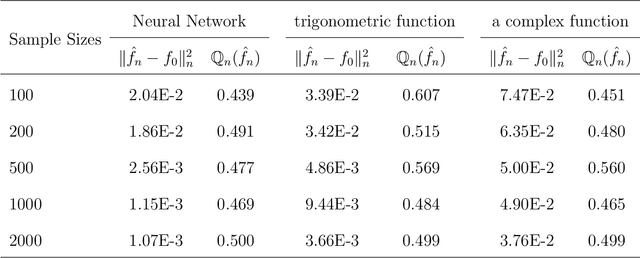
Neural networks have attracted a lot of attention due to its success in applications such as natural language processing and computer vision. For large scale data, due to the tremendous number of parameters in neural networks, overfitting is an issue in training neural networks. To avoid overfitting, one common approach is to penalize the parameters especially the weights in neural networks. Although neural networks has demonstrated its advantages in many applications, the theoretical foundation of penalized neural networks has not been well-established. Our goal of this paper is to propose the general framework of neural networks with regularization and prove its consistency. Under certain conditions, the estimated neural network will converge to true underlying function as the sample size increases. The method of sieves and the theory on minimal neural networks are used to overcome the issue of unidentifiability for the parameters. Two types of activation functions: hyperbolic tangent function(Tanh) and rectified linear unit(ReLU) have been taken into consideration. Simulations have been conducted to verify the validation of theorem of consistency.

A Neural Network Based Method with Transfer Learning for Genetic Data Analysis

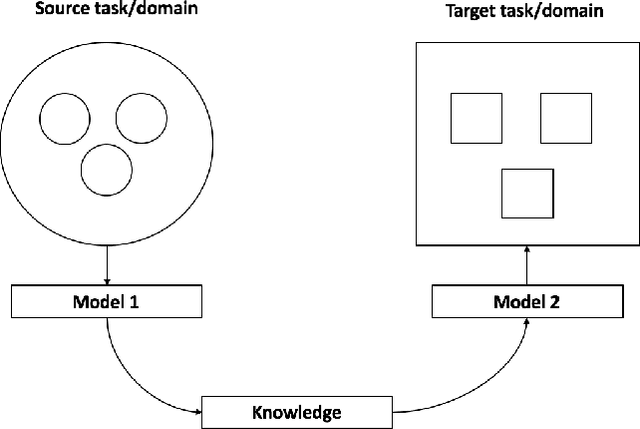
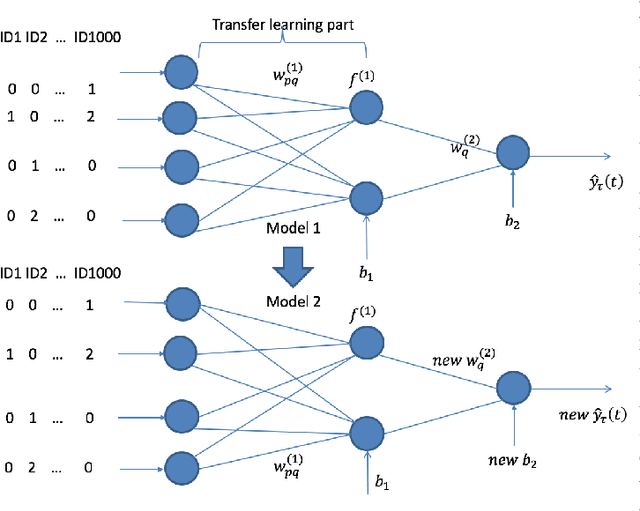
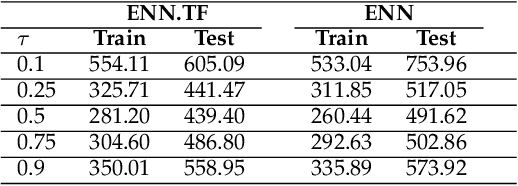
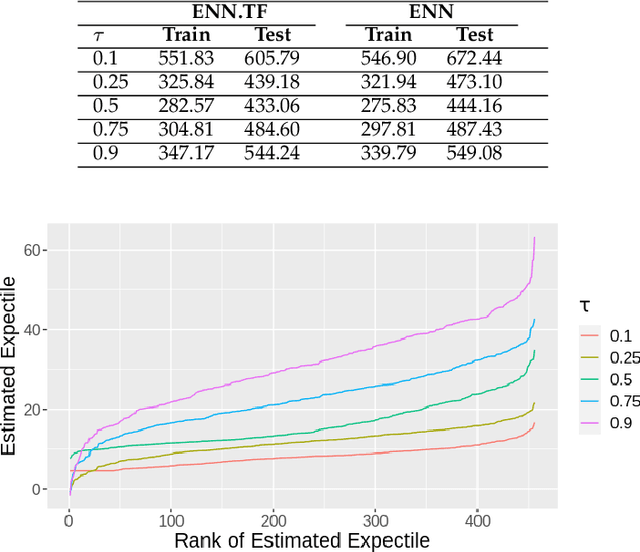
Transfer learning has emerged as a powerful technique in many application problems, such as computer vision and natural language processing. However, this technique is largely ignored in application to genetic data analysis. In this paper, we combine transfer learning technique with a neural network based method(expectile neural networks). With transfer learning, instead of starting the learning process from scratch, we start from one task that have been learned when solving a different task. We leverage previous learnings and avoid starting from scratch to improve the model performance by passing information gained in different but related task. To demonstrate the performance, we run two real data sets. By using transfer learning algorithm, the performance of expectile neural networks is improved compared to expectile neural network without using transfer learning technique.

Expectile Neural Networks for Genetic Data Analysis of Complex Diseases

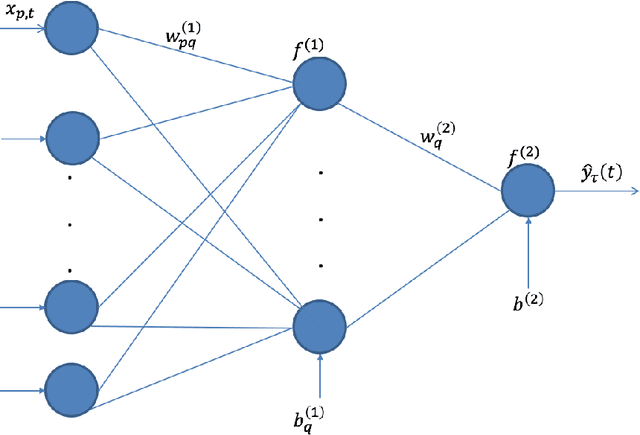
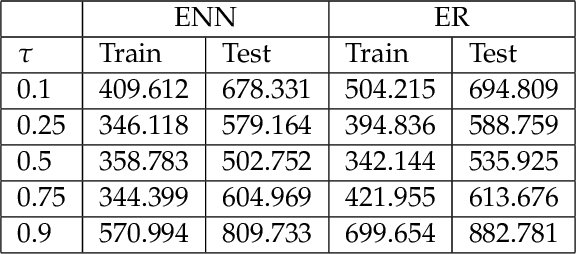
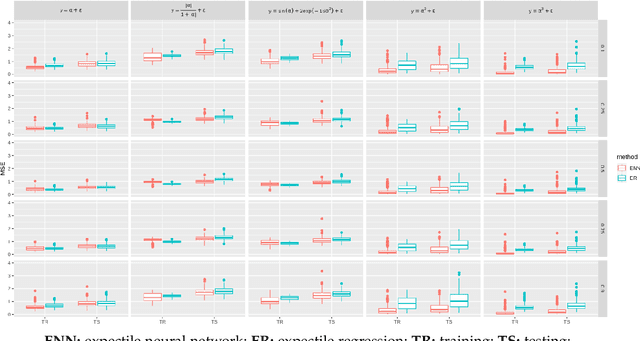
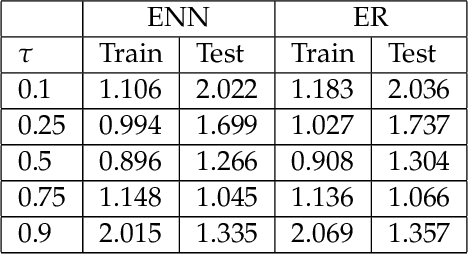
The genetic etiologies of common diseases are highly complex and heterogeneous. Classic statistical methods, such as linear regression, have successfully identified numerous genetic variants associated with complex diseases. Nonetheless, for most complex diseases, the identified variants only account for a small proportion of heritability. Challenges remain to discover additional variants contributing to complex diseases. Expectile regression is a generalization of linear regression and provides completed information on the conditional distribution of a phenotype of interest. While expectile regression has many nice properties and holds great promise for genetic data analyses (e.g., investigating genetic variants predisposing to a high-risk population), it has been rarely used in genetic research. In this paper, we develop an expectile neural network (ENN) method for genetic data analyses of complex diseases. Similar to expectile regression, ENN provides a comprehensive view of relationships between genetic variants and disease phenotypes and can be used to discover genetic variants predisposing to sub-populations (e.g., high-risk groups). We further integrate the idea of neural networks into ENN, making it capable of capturing non-linear and non-additive genetic effects (e.g., gene-gene interactions). Through simulations, we showed that the proposed method outperformed an existing expectile regression when there exist complex relationships between genetic variants and disease phenotypes. We also applied the proposed method to the genetic data from the Study of Addiction: Genetics and Environment(SAGE), investigating the relationships of candidate genes with smoking quantity.