A Sieve Quasi-likelihood Ratio Test for Neural Networks with Applications to Genetic Association Studies

Neural networks (NN) play a central role in modern Artificial intelligence (AI) technology and has been successfully used in areas such as natural language processing and image recognition. While majority of NN applications focus on prediction and classification, there are increasing interests in studying statistical inference of neural networks. The study of NN statistical inference can enhance our understanding of NN statistical proprieties. Moreover, it can facilitate the NN-based hypothesis testing that can be applied to hypothesis-driven clinical and biomedical research. In this paper, we propose a sieve quasi-likelihood ratio test based on NN with one hidden layer for testing complex associations. The test statistic has asymptotic chi-squared distribution, and therefore it is computationally efficient and easy for implementation in real data analysis. The validity of the asymptotic distribution is investigated via simulations. Finally, we demonstrate the use of the proposed test by performing a genetic association analysis of the sequencing data from Alzheimer's Disease Neuroimaging Initiative (ADNI).

Consistency of Neural Networks with Regularization

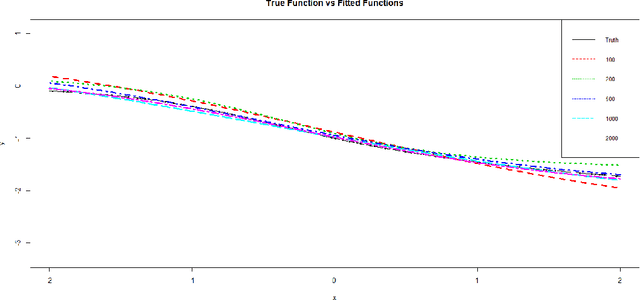
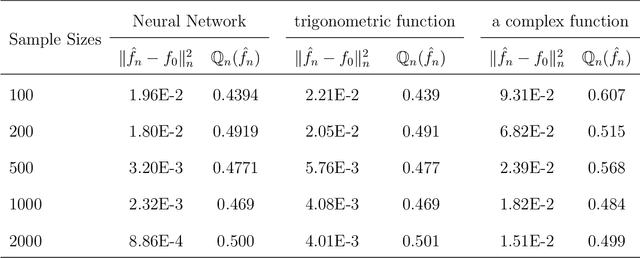
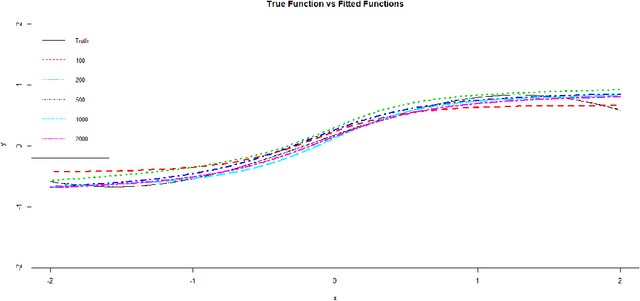
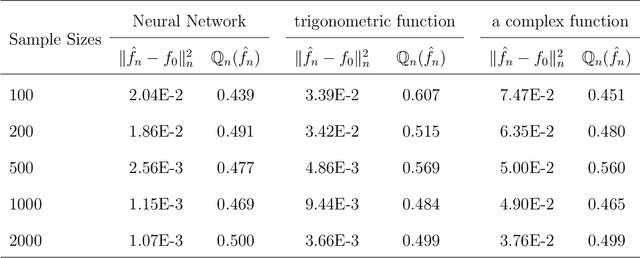
Neural networks have attracted a lot of attention due to its success in applications such as natural language processing and computer vision. For large scale data, due to the tremendous number of parameters in neural networks, overfitting is an issue in training neural networks. To avoid overfitting, one common approach is to penalize the parameters especially the weights in neural networks. Although neural networks has demonstrated its advantages in many applications, the theoretical foundation of penalized neural networks has not been well-established. Our goal of this paper is to propose the general framework of neural networks with regularization and prove its consistency. Under certain conditions, the estimated neural network will converge to true underlying function as the sample size increases. The method of sieves and the theory on minimal neural networks are used to overcome the issue of unidentifiability for the parameters. Two types of activation functions: hyperbolic tangent function(Tanh) and rectified linear unit(ReLU) have been taken into consideration. Simulations have been conducted to verify the validation of theorem of consistency.