ReMiDi: Reconstruction of Microstructure Using a Differentiable Diffusion MRI Simulator

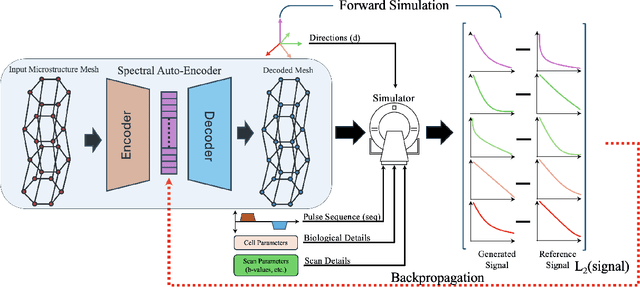
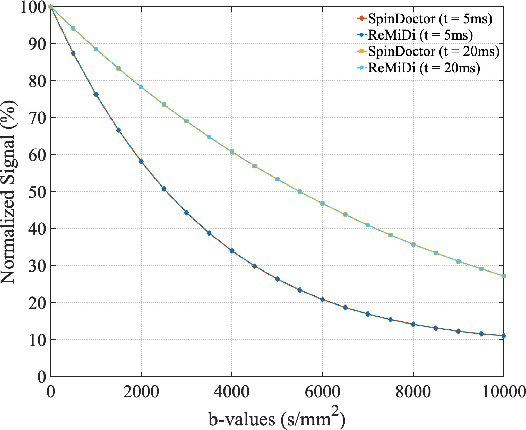
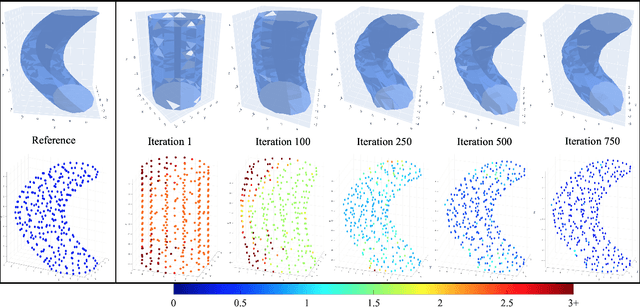
We propose ReMiDi, a novel method for inferring neuronal microstructure as arbitrary 3D meshes using a differentiable diffusion Magnetic Resonance Imaging (dMRI) simulator. We first implemented in PyTorch a differentiable dMRI simulator that simulates the forward diffusion process using a finite-element method on an input 3D microstructure mesh. To achieve significantly faster simulations, we solve the differential equation semi-analytically using a matrix formalism approach. Given a reference dMRI signal $S_{ref}$, we use the differentiable simulator to iteratively update the input mesh such that it matches $S_{ref}$ using gradient-based learning. Since directly optimizing the 3D coordinates of the vertices is challenging, particularly due to ill-posedness of the inverse problem, we instead optimize a lower-dimensional latent space representation of the mesh. The mesh is first encoded into spectral coefficients, which are further encoded into a latent $\textbf{z}$ using an auto-encoder, and are then decoded back into the true mesh. We present an end-to-end differentiable pipeline that simulates signals that can be tuned to match a reference signal by iteratively updating the latent representation $\textbf{z}$. We demonstrate the ability to reconstruct microstructures of arbitrary shapes represented by finite-element meshes, with a focus on axonal geometries found in the brain white matter, including bending, fanning and beading fibers. Our source code will be made available online.

Three-dimensional micro-structurally informed in silico myocardium -- towards virtual imaging trials in cardiac diffusion weighted MRI

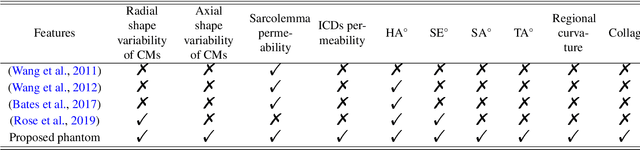
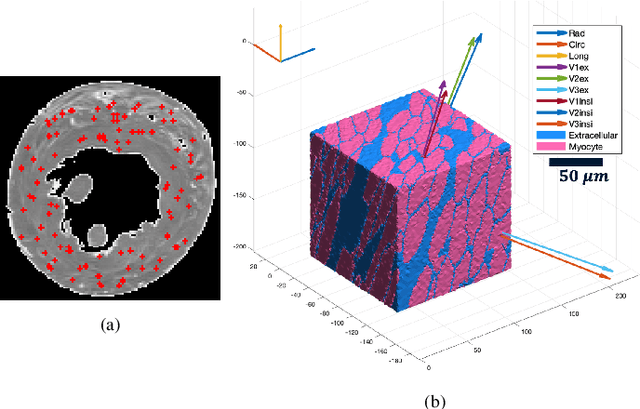
In silico tissue models enable evaluating quantitative models of magnetic resonance imaging. This includes validating and sensitivity analysis of imaging biomarkers and tissue microstructure parameters. We propose a novel method to generate a realistic numerical phantom of myocardial microstructure. We extend previous studies accounting for the cardiomyocyte shape variability, water exchange between the cardiomyocytes (intercalated discs), myocardial microstructure disarray, and four sheetlet orientations. In the first stage of the method, cardiomyocytes and sheetlets are generated by considering the shape variability and intercalated discs in cardiomyocyte-to-cardiomyocyte connections. Sheetlets are then aggregated and oriented in the directions of interest. Our morphometric study demonstrates no significant difference ($p>0.01$) between the distribution of volume, length, and primary and secondary axes of the numerical and real (literature) cardiomyocyte data. Structural correlation analysis validates that the in-silico tissue is in the same class of disorderliness as the real tissue. Additionally, the absolute angle differences between the simulated helical angle (HA) and input HA (reference value) of the cardiomyocytes ($4.3^\circ\pm 3.1^\circ$) demonstrate a good agreement with the absolute angle difference between the measured HA using experimental cardiac diffusion tensor imaging (cDTI) and histology (reference value) reported by (Holmes et al., 2000) ($3.7^\circ\pm6.4^\circ$) and (Scollan et al., 1998) ($4.9^\circ\pm 14.6^\circ$). The angular distance between eigenvectors and sheetlet angles of the input and simulated cDTI is smaller than those between measured angles using structural tensor imaging (gold standard) and experimental cDTI. These results confirm that the proposed method can generate richer numerical phantoms for the myocardium than previous studies.