Group structure estimation for panel data -- a general approach

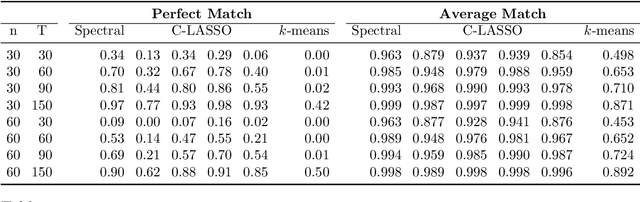
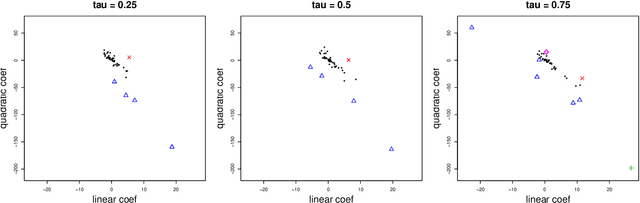
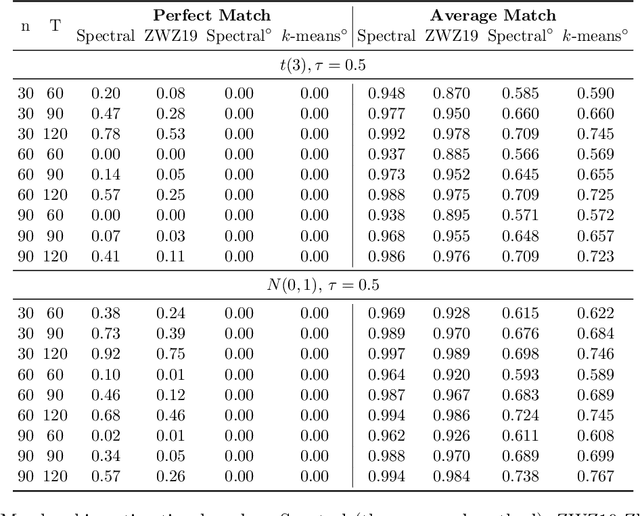
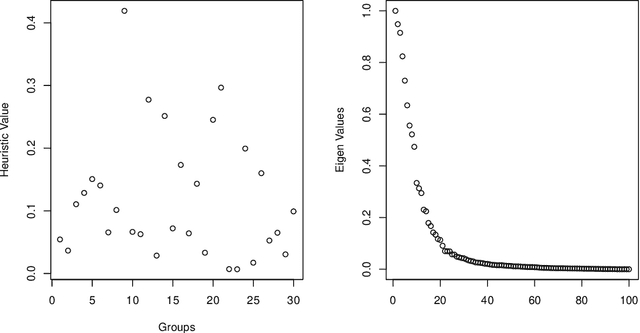
Consider a panel data setting where repeated observations on individuals are available. Often it is reasonable to assume that there exist groups of individuals that share similar effects of observed characteristics, but the grouping is typically unknown in advance. We propose a novel approach to estimate such unobserved groupings for general panel data models. Our method explicitly accounts for the uncertainty in individual parameter estimates and remains computationally feasible with a large number of individuals and/or repeated measurements on each individual. The developed ideas can be applied even when individual-level data are not available and only parameter estimates together with some quantification of uncertainty are given to the researcher.

Learning big Gaussian Bayesian networks: partition, estimation, and fusion

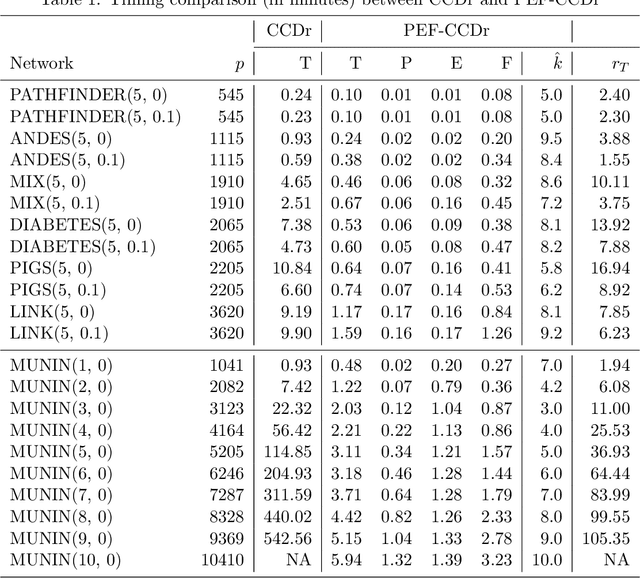
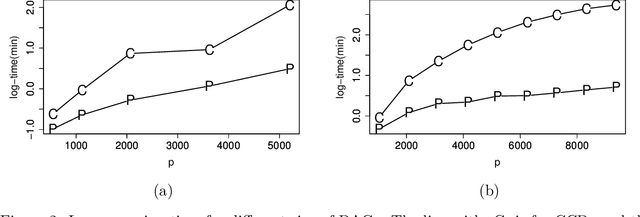
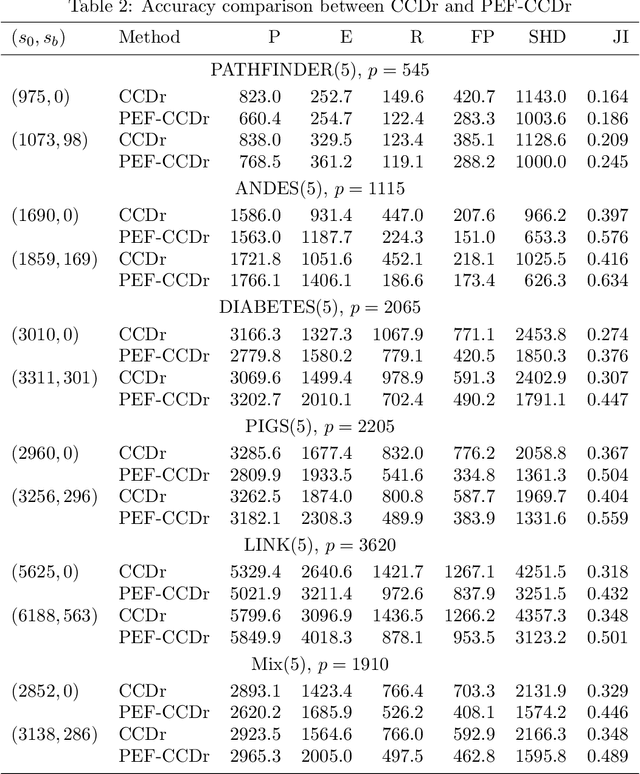
Structure learning of Bayesian networks has always been a challenging problem. Nowadays, massive-size networks with thousands or more of nodes but fewer samples frequently appear in many areas. We develop a divide-and-conquer framework, called partition-estimation-fusion (PEF), for structure learning of such big networks. The proposed method first partitions nodes into clusters, then learns a subgraph on each cluster of nodes, and finally fuses all learned subgraphs into one Bayesian network. The PEF method is designed in a flexible way so that any structure learning method may be used in the second step to learn a subgraph structure as either a DAG or a CPDAG. In the clustering step, we adapt the hierarchical clustering method to automatically choose a proper number of clusters. In the fusion step, we propose a novel hybrid method that sequentially add edges between subgraphs. Extensive numerical experiments demonstrate the competitive performance of our PEF method, in terms of both speed and accuracy compared to existing methods. Our method can improve the accuracy of structure learning by 20% or more, while reducing running time up to two orders-of-magnitude.

Learning Large-Scale Bayesian Networks with the sparsebn Package

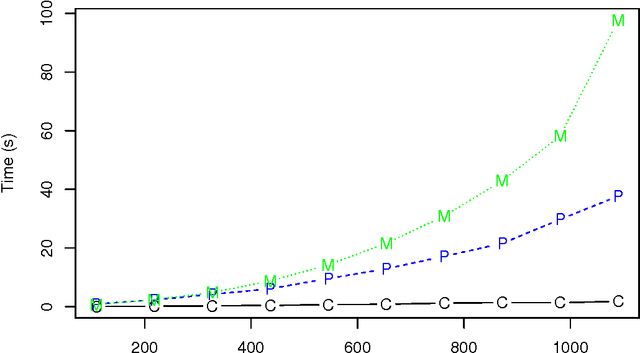
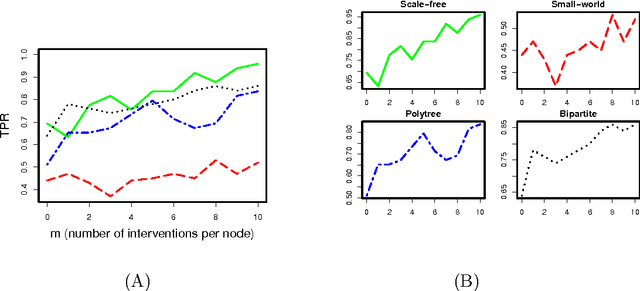
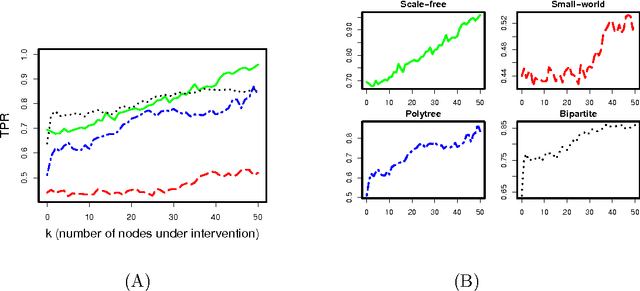
Learning graphical models from data is an important problem with wide applications, ranging from genomics to the social sciences. Nowadays datasets often have upwards of thousands---sometimes tens or hundreds of thousands---of variables and far fewer samples. To meet this challenge, we have developed a new R package called sparsebn for learning the structure of large, sparse graphical models with a focus on Bayesian networks. While there are many existing software packages for this task, this package focuses on the unique setting of learning large networks from high-dimensional data, possibly with interventions. As such, the methods provided place a premium on scalability and consistency in a high-dimensional setting. Furthermore, in the presence of interventions, the methods implemented here achieve the goal of learning a causal network from data. Additionally, the sparsebn package is fully compatible with existing software packages for network analysis.

Penalized Estimation of Directed Acyclic Graphs From Discrete Data

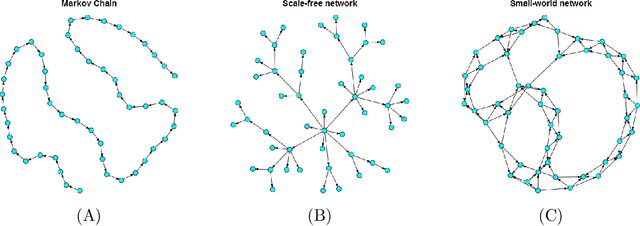
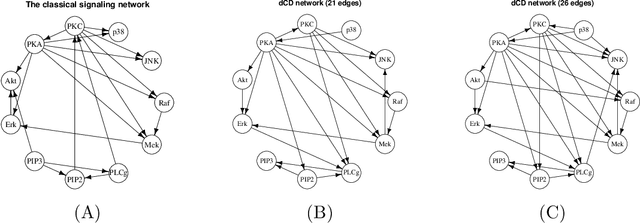
Bayesian networks, with structure given by a directed acyclic graph (DAG), are a popular class of graphical models. However, learning Bayesian networks from discrete or categorical data is particularly challenging, due to the large parameter space and the difficulty in searching for a sparse structure. In this article, we develop a maximum penalized likelihood method to tackle this problem. Instead of the commonly used multinomial distribution, we model the conditional distribution of a node given its parents by multi-logit regression, in which an edge is parameterized by a set of coefficient vectors with dummy variables encoding the levels of a node. To obtain a sparse DAG, a group norm penalty is employed, and a blockwise coordinate descent algorithm is developed to maximize the penalized likelihood subject to the acyclicity constraint of a DAG. When interventional data are available, our method constructs a causal network, in which a directed edge represents a causal relation. We apply our method to various simulated and real data sets. The results show that our method is very competitive, compared to many existing methods, in DAG estimation from both interventional and high-dimensional observational data.