A Unified Model for the Two-stage Offline-then-Online Resource Allocation

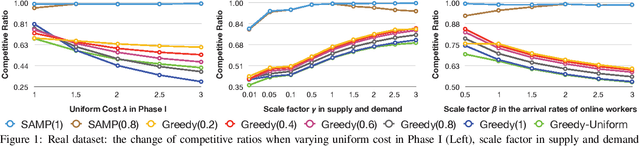
With the popularity of the Internet, traditional offline resource allocation has evolved into a new form, called online resource allocation. It features the online arrivals of agents in the system and the real-time decision-making requirement upon the arrival of each online agent. Both offline and online resource allocation have wide applications in various real-world matching markets ranging from ridesharing to crowdsourcing. There are some emerging applications such as rebalancing in bike sharing and trip-vehicle dispatching in ridesharing, which involve a two-stage resource allocation process. The process consists of an offline phase and another sequential online phase, and both phases compete for the same set of resources. In this paper, we propose a unified model which incorporates both offline and online resource allocation into a single framework. Our model assumes non-uniform and known arrival distributions for online agents in the second online phase, which can be learned from historical data. We propose a parameterized linear programming (LP)-based algorithm, which is shown to be at most a constant factor of $1/4$ from the optimal. Experimental results on the real dataset show that our LP-based approaches outperform the LP-agnostic heuristics in terms of robustness and effectiveness.

Thompson Sampling for Combinatorial Semi-bandits with Sleeping Arms and Long-Term Fairness Constraints

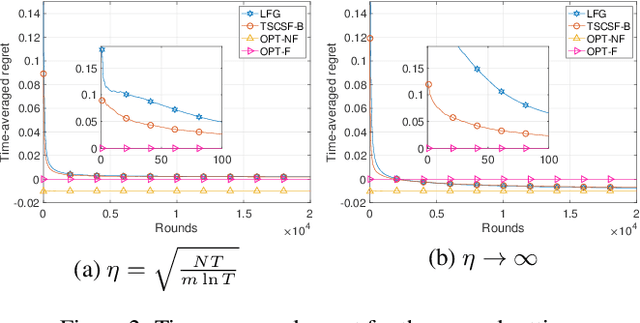
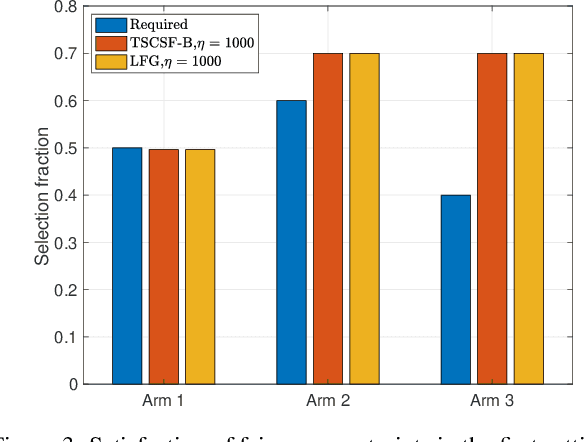
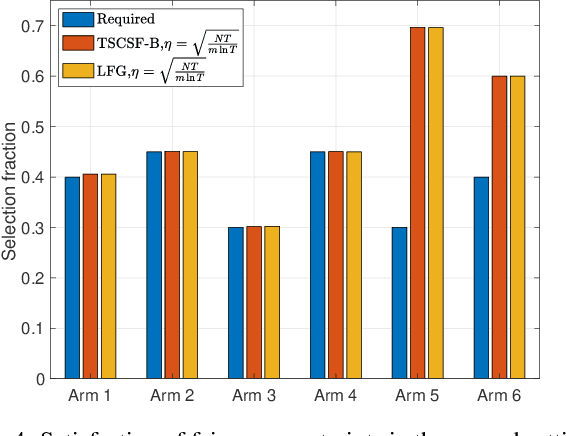
We study the combinatorial sleeping multi-armed semi-bandit problem with long-term fairness constraints~(CSMAB-F). To address the problem, we adopt Thompson Sampling~(TS) to maximize the total rewards and use virtual queue techniques to handle the fairness constraints, and design an algorithm called \emph{TS with beta priors and Bernoulli likelihoods for CSMAB-F~(TSCSF-B)}. Further, we prove TSCSF-B can satisfy the fairness constraints, and the time-averaged regret is upper bounded by $\frac{N}{2\eta} + O\left(\frac{\sqrt{mNT\ln T}}{T}\right)$, where $N$ is the total number of arms, $m$ is the maximum number of arms that can be pulled simultaneously in each round~(the cardinality constraint) and $\eta$ is the parameter trading off fairness for rewards. By relaxing the fairness constraints (i.e., let $\eta \rightarrow \infty$), the bound boils down to the first problem-independent bound of TS algorithms for combinatorial sleeping multi-armed semi-bandit problems. Finally, we perform numerical experiments and use a high-rating movie recommendation application to show the effectiveness and efficiency of the proposed algorithm.