Are Outlier Detection Methods Resilient to Sampling?

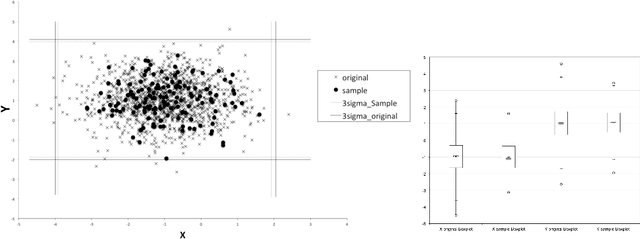
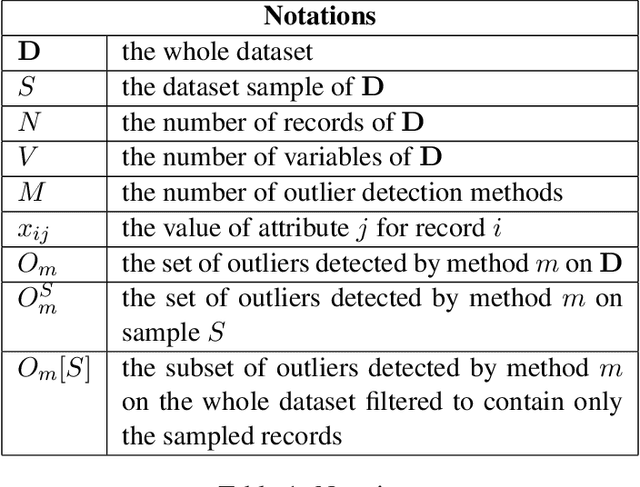
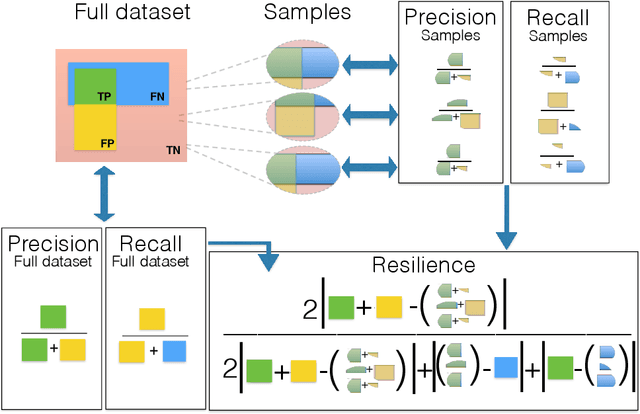
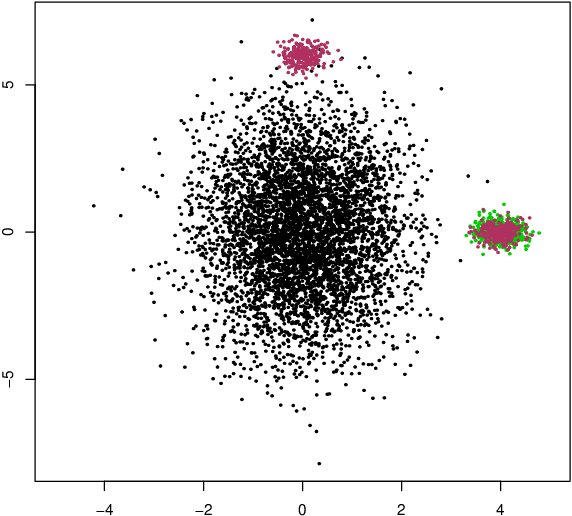
Outlier detection is a fundamental task in data mining and has many applications including detecting errors in databases. While there has been extensive prior work on methods for outlier detection, modern datasets often have sizes that are beyond the ability of commonly used methods to process the data within a reasonable time. To overcome this issue, outlier detection methods can be trained over samples of the full-sized dataset. However, it is not clear how a model trained on a sample compares with one trained on the entire dataset. In this paper, we introduce the notion of resilience to sampling for outlier detection methods. Orthogonal to traditional performance metrics such as precision/recall, resilience represents the extent to which the outliers detected by a method applied to samples from a sampling scheme matches those when applied to the whole dataset. We propose a novel approach for estimating the resilience to sampling of both individual outlier methods and their ensembles. We performed an extensive experimental study on synthetic and real-world datasets where we study seven diverse and representative outlier detection methods, compare results obtained from samples versus those obtained from the whole datasets and evaluate the accuracy of our resilience estimates. We observed that the methods are not equally resilient to a given sampling scheme and it is often the case that careful joint selection of both the sampling scheme and the outlier detection method is necessary. It is our hope that the paper initiates research on designing outlier detection algorithms that are resilient to sampling.

Regression shrinkage and grouping of highly correlated predictors with HORSES

Identifying homogeneous subgroups of variables can be challenging in high dimensional data analysis with highly correlated predictors. We propose a new method called Hexagonal Operator for Regression with Shrinkage and Equality Selection, HORSES for short, that simultaneously selects positively correlated variables and identifies them as predictive clusters. This is achieved via a constrained least-squares problem with regularization that consists of a linear combination of an L_1 penalty for the coefficients and another L_1 penalty for pairwise differences of the coefficients. This specification of the penalty function encourages grouping of positively correlated predictors combined with a sparsity solution. We construct an efficient algorithm to implement the HORSES procedure. We show via simulation that the proposed method outperforms other variable selection methods in terms of prediction error and parsimony. The technique is demonstrated on two data sets, a small data set from analysis of soil in Appalachia, and a high dimensional data set from a near infrared (NIR) spectroscopy study, showing the flexibility of the methodology.