Analyzing social media with crowdsourcing in Crowd4SDG

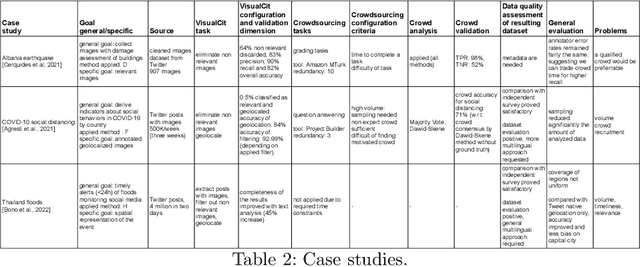
Social media have the potential to provide timely information about emergency situations and sudden events. However, finding relevant information among millions of posts being posted every day can be difficult, and developing a data analysis project usually requires time and technical skills. This study presents an approach that provides flexible support for analyzing social media, particularly during emergencies. Different use cases in which social media analysis can be adopted are introduced, and the challenges of retrieving information from large sets of posts are discussed. The focus is on analyzing images and text contained in social media posts and a set of automatic data processing tools for filtering, classification, and geolocation of content with a human-in-the-loop approach to support the data analyst. Such support includes both feedback and suggestions to configure automated tools, and crowdsourcing to gather inputs from citizens. The results are validated by discussing three case studies developed within the Crowd4SDG H2020 European project.

A first approach to closeness distributions

Probabilistic graphical models allow us to encode a large probability distribution as a composition of smaller ones. It is oftentimes the case that we are interested in incorporating in the model the idea that some of these smaller distributions are likely to be similar to one another. In this paper we provide an information geometric approach on how to incorporate this information, and see that it allows us to reinterpret some already existing models.

Parametrization invariant interpretation of priors and posteriors

In this paper we leverage on probability over Riemannian manifolds to rethink the interpretation of priors and posteriors in Bayesian inference. The main mindshift is to move away from the idea that "a prior distribution establishes a probability distribution over the parameters of our model" to the idea that "a prior distribution establishes a probability distribution over probability distributions". To do that we assume that our probabilistic model is a Riemannian manifold with the Fisher metric. Under this mindset, any distribution over probability distributions should be "intrinsic", that is, invariant to the specific parametrization which is selected for the manifold. We exemplify our ideas through a simple analysis of distributions over the manifold of Bernoulli distributions. One of the major shortcomings of maximum a posteriori estimates is that they depend on the parametrization. Based on the understanding developed here, we can define the maximum a posteriori estimate which is independent of the parametrization.

Decentralized dynamic task allocation for UAVs with limited communication range

We present the Limited-range Online Routing Problem (LORP), which involves a team of Unmanned Aerial Vehicles (UAVs) with limited communication range that must autonomously coordinate to service task requests. We first show a general approach to cast this dynamic problem as a sequence of decentralized task allocation problems. Then we present two solutions both based on modeling the allocation task as a Markov Random Field to subsequently assess decisions by means of the decentralized Max-Sum algorithm. Our first solution assumes independence between requests, whereas our second solution also considers the UAVs' workloads. A thorough empirical evaluation shows that our workload-based solution consistently outperforms current state-of-the-art methods in a wide range of scenarios, lowering the average service time up to 16%. In the best-case scenario there is no gap between our decentralized solution and centralized techniques. In the worst-case scenario we manage to reduce by 25% the gap between current decentralized and centralized techniques. Thus, our solution becomes the method of choice for our problem.

Sufficient and necessary conditions for Dynamic Programming in Valuation-Based Systems

Valuation algebras abstract a large number of formalisms for automated reasoning and enable the definition of generic inference procedures. Many of these formalisms provide some notion of solution. Typical examples are satisfying assignments in constraint systems, models in logics or solutions to linear equation systems. Many widely used dynamic programming algorithms for optimization problems rely on low treewidth decompositions and can be understood as particular cases of a single algorithmic scheme for finding solutions in a valuation algebra. The most encompassing description of this algorithmic scheme to date has been proposed by Pouly and Kohlas together with sufficient conditions for its correctness. Unfortunately, the formalization relies on a theorem for which we provide counterexamples. In spite of that, the mainline of Pouly and Kohlas' theory is correct, although some of the necessary conditions have to be revised. In this paper we analyze the impact that the counter-examples have on the theory, and rebuild the theory providing correct sufficient conditions for the algorithms. Furthermore, we also provide necessary conditions for the algorithms, allowing for a sharper characterization of when the algorithmic scheme can be applied.

Even more generic solution construction in Valuation-Based Systems

Valuation algebras abstract a large number of formalisms for automated reasoning and enable the definition of generic inference procedures. Many of these formalisms provide some notions of solutions. Typical examples are satisfying assignments in constraint systems, models in logics or solutions to linear equation systems. Recently, formal requirements for the presence of solutions and a generic algorithm for solution construction based on the results of a previously executed inference scheme have been proposed in the literature. Unfortunately, the formalization of Pouly and Kohlas relies on a theorem for which we provide a counter example. In spite of that, the mainline of the theory described is correct, although some of the necessary conditions to apply some of the algorithms have to be revised. To fix the theory, we generalize some of their definitions and provide correct sufficient conditions for the algorithms. As a result, we get a more general and corrected version of the already existing theory.

Bayesian Conditional Gaussian Network Classifiers with Applications to Mass Spectra Classification

Classifiers based on probabilistic graphical models are very effective. In continuous domains, maximum likelihood is usually used to assess the predictions of those classifiers. When data is scarce, this can easily lead to overfitting. In any probabilistic setting, Bayesian averaging (BA) provides theoretically optimal predictions and is known to be robust to overfitting. In this work we introduce Bayesian Conditional Gaussian Network Classifiers, which efficiently perform exact Bayesian averaging over the parameters. We evaluate the proposed classifiers against the maximum likelihood alternatives proposed so far over standard UCI datasets, concluding that performing BA improves the quality of the assessed probabilities (conditional log likelihood) whilst maintaining the error rate. Overfitting is more likely to occur in domains where the number of data items is small and the number of variables is large. These two conditions are met in the realm of bioinformatics, where the early diagnosis of cancer from mass spectra is a relevant task. We provide an application of our classification framework to that problem, comparing it with the standard maximum likelihood alternative, where the improvement of quality in the assessed probabilities is confirmed.