Learning the Factors Controlling Mineralization for Geologic Carbon Sequestration

We perform a set of flow and reactive transport simulations within three-dimensional fracture networks to learn the factors controlling mineral reactions. CO$_2$ mineralization requires CO$_2$-laden water, dissolution of a mineral that then leads to precipitation of a CO$_2$-bearing mineral. Our discrete fracture networks (DFN) are partially filled with quartz that gradually dissolves until it reaches a quasi-steady state. At the end of the simulation, we measure the quartz remaining in each fracture within the domain. We observe that a small backbone of fracture exists, where the quartz is fully dissolved which leads to increased flow and transport. However, depending on the DFN topology and the rate of dissolution, we observe a large variability of these changes, which indicates an interplay between the fracture network structure and the impact of geochemical dissolution. In this work, we developed a machine learning framework to extract the important features that support mineralization in the form of dissolution. In addition, we use structural and topological features of the fracture network to predict the remaining quartz volume in quasi-steady state conditions. As a first step to characterizing carbon mineralization, we study dissolution with this framework. We studied a variety of reaction and fracture parameters and their impact on the dissolution of quartz in fracture networks. We found that the dissolution reaction rate constant of quartz and the distance to the flowing backbone in the fracture network are the two most important features that control the amount of quartz left in the system. For the first time, we use a combination of a finite-volume reservoir model and graph-based approach to study reactive transport in a complex fracture network to determine the key features that control dissolution.

Sensitivity Analysis in the Presence of Intrinsic Stochasticity for Discrete Fracture Network Simulations

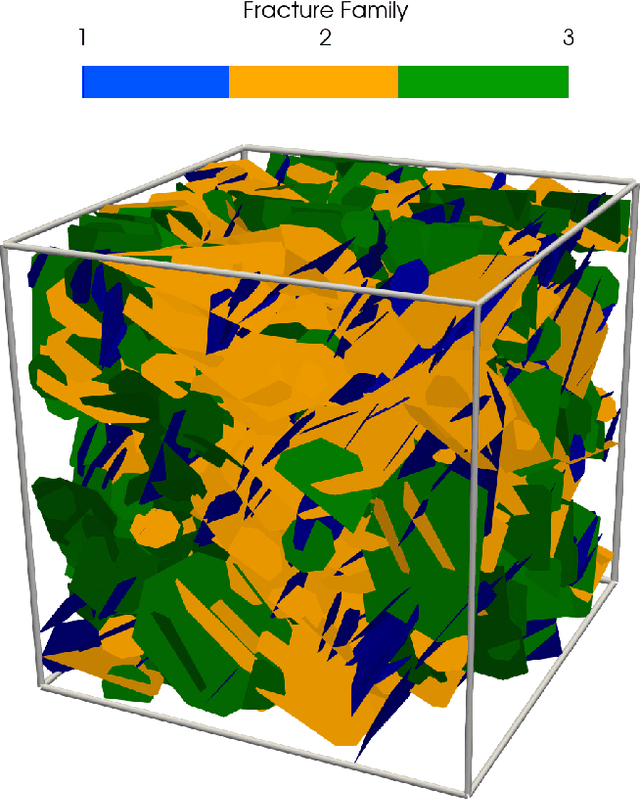
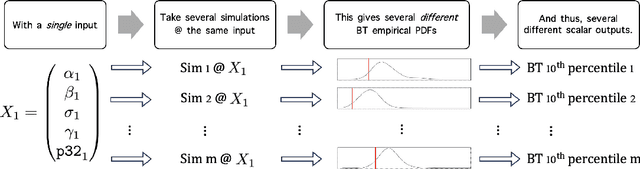
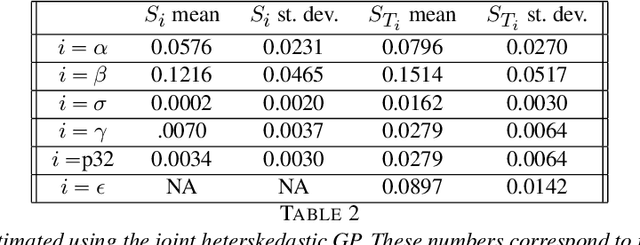
Large-scale discrete fracture network (DFN) simulators are standard fare for studies involving the sub-surface transport of particles since direct observation of real world underground fracture networks is generally infeasible. While these simulators have seen numerous successes over several engineering applications, estimations on quantities of interest (QoI) - such as breakthrough time of particles reaching the edge of the system - suffer from a two distinct types of uncertainty. A run of a DFN simulator requires several parameter values to be set that dictate the placement and size of fractures, the density of fractures, and the overall permeability of the system; uncertainty on the proper parameter choices will lead to some amount of uncertainty in the QoI, called epistemic uncertainty. Furthermore, since DFN simulators rely on stochastic processes to place fractures and govern flow, understanding how this randomness affects the QoI requires several runs of the simulator at distinct random seeds. The uncertainty in the QoI attributed to different realizations (i.e. different seeds) of the same random process leads to a second type of uncertainty, called aleatoric uncertainty. In this paper, we perform a Sensitivity Analysis, which directly attributes the uncertainty observed in the QoI to the epistemic uncertainty from each input parameter and to the aleatoric uncertainty. We make several design choices to handle an observed heteroskedasticity in DFN simulators, where the aleatoric uncertainty changes for different inputs, since the quality makes several standard statistical methods inadmissible. Beyond the specific takeaways on which input variables affect uncertainty the most for DFN simulators, a major contribution of this paper is the introduction of a statistically rigorous workflow for characterizing the uncertainty in DFN flow simulations that exhibit heteroskedasticity.

Machine learning for graph-based representations of three-dimensional discrete fracture networks

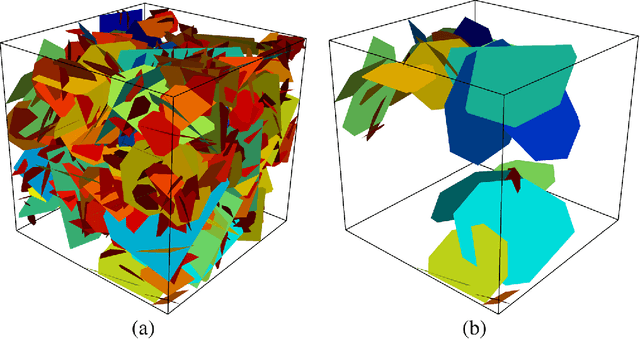
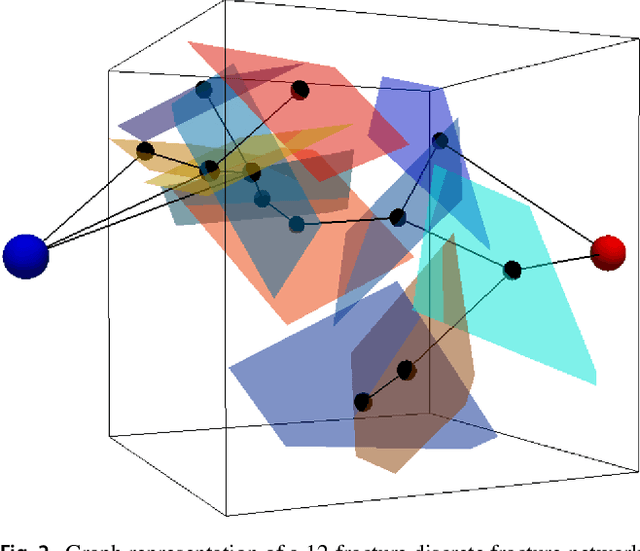
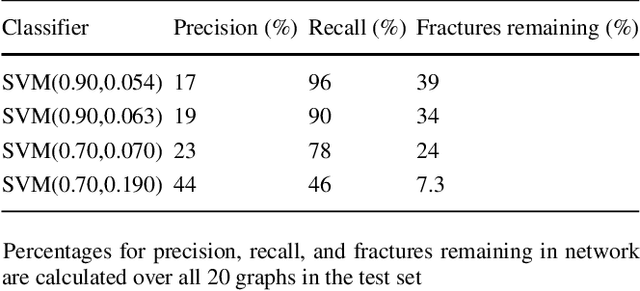
Structural and topological information play a key role in modeling flow and transport through fractured rock in the subsurface. Discrete fracture network (DFN) computational suites such as dfnWorks are designed to simulate flow and transport in such porous media. Flow and transport calculations reveal that a small backbone of fractures exists, where most flow and transport occurs. Restricting the flowing fracture network to this backbone provides a significant reduction in the network's effective size. However, the particle tracking simulations needed to determine the reduction are computationally intensive. Such methods may be impractical for large systems or for robust uncertainty quantification of fracture networks, where thousands of forward simulations are needed to bound system behavior. In this paper, we develop an alternative network reduction approach to characterizing transport in DFNs, by combining graph theoretical and machine learning methods. We consider a graph representation where nodes signify fractures and edges denote their intersections. Using random forest and support vector machines, we rapidly identify a subnetwork that captures the flow patterns of the full DFN, based primarily on node centrality features in the graph. Our supervised learning techniques train on particle-tracking backbone paths found by dfnWorks, but run in negligible time compared to those simulations. We find that our predictions can reduce the network to approximately 20% of its original size, while still generating breakthrough curves consistent with those of the original network.