Javier V. Gomez
An Asymptotically-Optimal Sampling-Based Algorithm for Bi-directional Motion Planning
Jul 27, 2015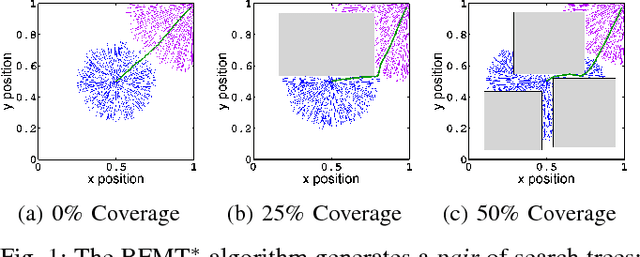
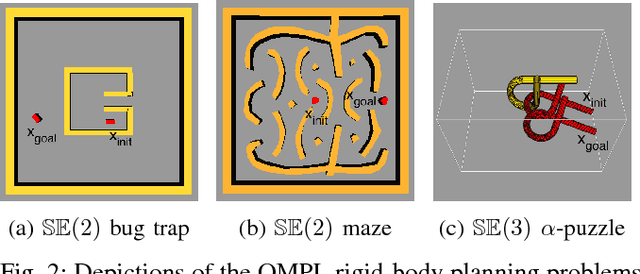
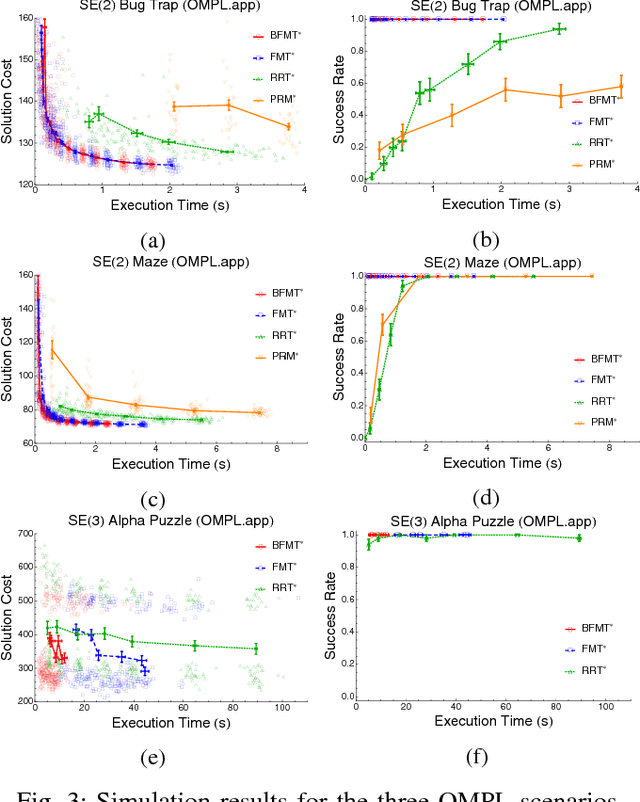
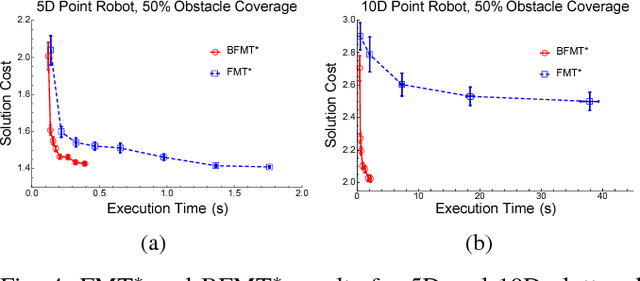
Abstract:Bi-directional search is a widely used strategy to increase the success and convergence rates of sampling-based motion planning algorithms. Yet, few results are available that merge both bi-directional search and asymptotic optimality into existing optimal planners, such as PRM*, RRT*, and FMT*. The objective of this paper is to fill this gap. Specifically, this paper presents a bi-directional, sampling-based, asymptotically-optimal algorithm named Bi-directional FMT* (BFMT*) that extends the Fast Marching Tree (FMT*) algorithm to bi-directional search while preserving its key properties, chiefly lazy search and asymptotic optimality through convergence in probability. BFMT* performs a two-source, lazy dynamic programming recursion over a set of randomly-drawn samples, correspondingly generating two search trees: one in cost-to-come space from the initial configuration and another in cost-to-go space from the goal configuration. Numerical experiments illustrate the advantages of BFMT* over its unidirectional counterpart, as well as a number of other state-of-the-art planners.
Fast Methods for Eikonal Equations: an Experimental Survey
Jun 11, 2015

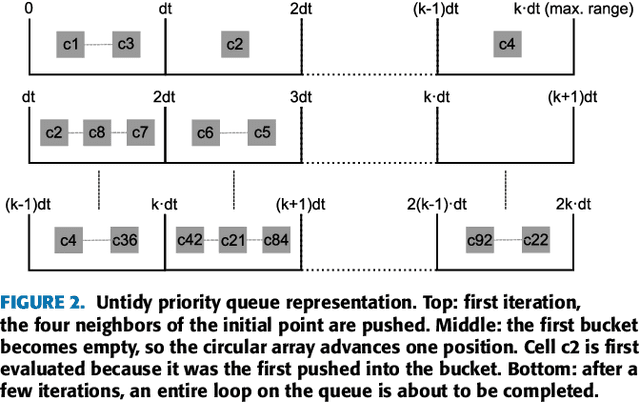
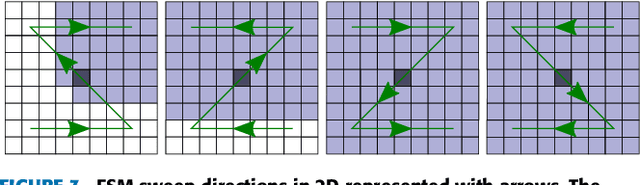
Abstract:The Fast Marching Method is a very popular algorithm to compute times-of-arrival maps (distances map measured in time units). Since their proposal in 1995, it has been applied to many different applications such as robotics, medical computer vision, fluid simulation, etc. Many alternatives have been proposed with two main objectives: to reduce its computational time and to improve its accuracy. In this paper, we collect the main approaches which improve the computational time of the standard Fast Marching Method, focusing on single-threaded methods and isotropic environments. 9 different methods are studied under a common mathematical framework and experimentally in representative environments: Fast Marching Method with binary heap, Fast Marching Method with Fibonacci Heap, Simplified Fast Marching Method, Untidy Fast Marching Method, Fast Iterative Method, Group Marching Method, Fast Sweeping Method, Lock Sweeping Method and Double Dynamic Queue Method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge