k-Means Clustering and Ensemble of Regressions: An Algorithm for the ISIC 2017 Skin Lesion Segmentation Challenge

This abstract briefly describes a segmentation algorithm developed for the ISIC 2017 Skin Lesion Detection Competition hosted at [ref]. The objective of the competition is to perform a segmentation (in the form of a binary mask image) of skin lesions in dermoscopic images as close as possible to a segmentation performed by trained clinicians, which is taken as ground truth. This project only takes part in the segmentation phase of the challenge. The other phases of the competition (feature extraction and lesion identification) are not considered. The proposed algorithm consists of 4 steps: (1) lesion image preprocessing, (2) image segmentation using k-means clustering of pixel colors, (3) calculation of a set of features describing the properties of each segmented region, and (4) calculation of a final score for each region, representing the likelihood of corresponding to a suitable lesion segmentation. The scores in step (4) are obtained by averaging the results of 2 different regression models using the scores of each region as input. Before using the algorithm these regression models must be trained using the training set of images and ground truth masks provided by the Competition. Steps 2 to 4 are repeated with an increasing number of clusters (and therefore the image is segmented into more regions) until there is no further improvement of the calculated scores.

Fast Methods for Eikonal Equations: an Experimental Survey

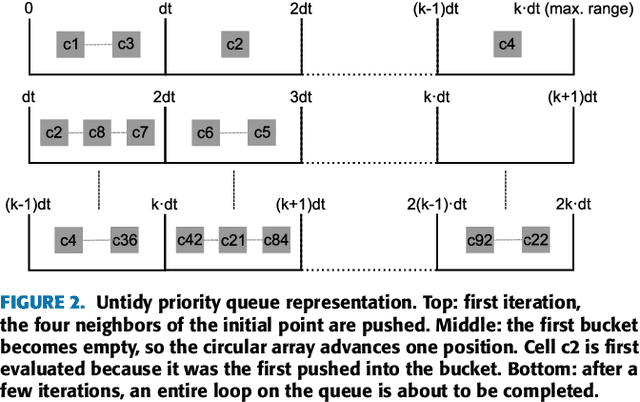
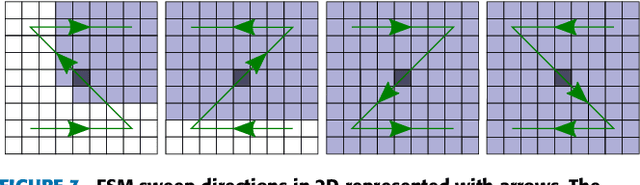
The Fast Marching Method is a very popular algorithm to compute times-of-arrival maps (distances map measured in time units). Since their proposal in 1995, it has been applied to many different applications such as robotics, medical computer vision, fluid simulation, etc. Many alternatives have been proposed with two main objectives: to reduce its computational time and to improve its accuracy. In this paper, we collect the main approaches which improve the computational time of the standard Fast Marching Method, focusing on single-threaded methods and isotropic environments. 9 different methods are studied under a common mathematical framework and experimentally in representative environments: Fast Marching Method with binary heap, Fast Marching Method with Fibonacci Heap, Simplified Fast Marching Method, Untidy Fast Marching Method, Fast Iterative Method, Group Marching Method, Fast Sweeping Method, Lock Sweeping Method and Double Dynamic Queue Method.