Joseph A. Starek
An Asymptotically-Optimal Sampling-Based Algorithm for Bi-directional Motion Planning
Jul 27, 2015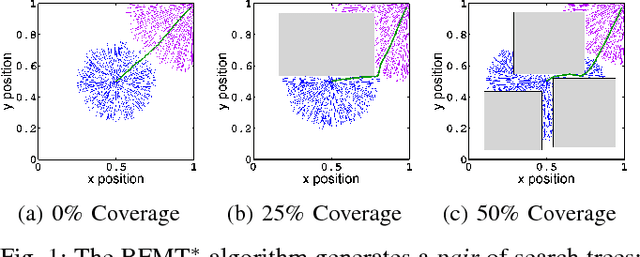
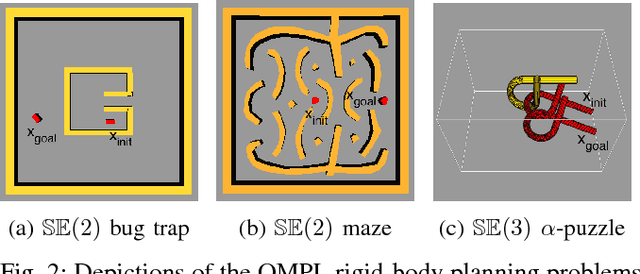
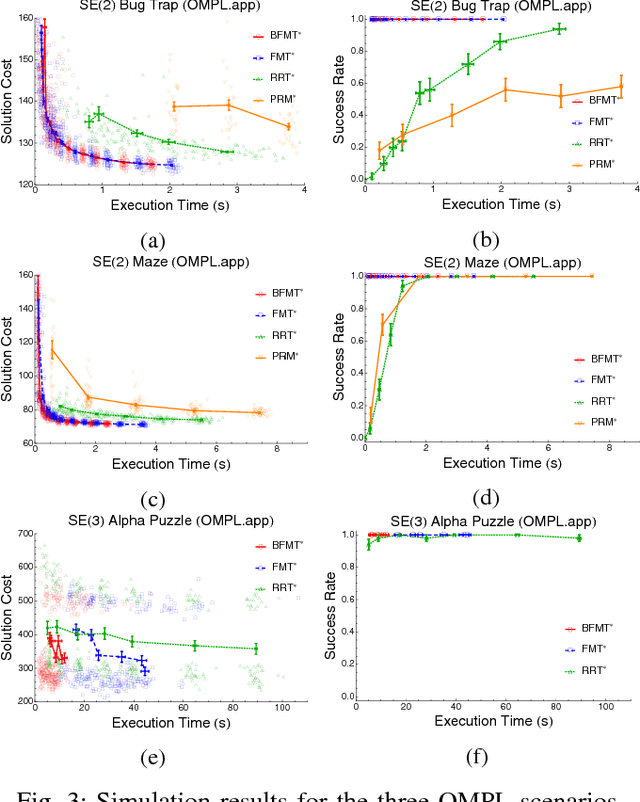
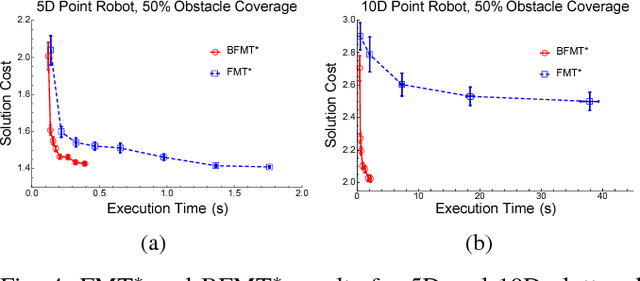
Abstract:Bi-directional search is a widely used strategy to increase the success and convergence rates of sampling-based motion planning algorithms. Yet, few results are available that merge both bi-directional search and asymptotic optimality into existing optimal planners, such as PRM*, RRT*, and FMT*. The objective of this paper is to fill this gap. Specifically, this paper presents a bi-directional, sampling-based, asymptotically-optimal algorithm named Bi-directional FMT* (BFMT*) that extends the Fast Marching Tree (FMT*) algorithm to bi-directional search while preserving its key properties, chiefly lazy search and asymptotic optimality through convergence in probability. BFMT* performs a two-source, lazy dynamic programming recursion over a set of randomly-drawn samples, correspondingly generating two search trees: one in cost-to-come space from the initial configuration and another in cost-to-go space from the goal configuration. Numerical experiments illustrate the advantages of BFMT* over its unidirectional counterpart, as well as a number of other state-of-the-art planners.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge