Robustness quantification and how it allows for reliable classification, even in the presence of distribution shift and for small training sets

Based on existing ideas in the field of imprecise probabilities, we present a new approach for assessing the reliability of the individual predictions of a generative probabilistic classifier. We call this approach robustness quantification, compare it to uncertainty quantification, and demonstrate that it continues to work well even for classifiers that are learned from small training sets that are sampled from a shifted distribution.

A decision-theoretic approach to dealing with uncertainty in quantum mechanics

We provide a decision-theoretic framework for dealing with uncertainty in quantum mechanics. This uncertainty is two-fold: on the one hand there may be uncertainty about the state the quantum system is in, and on the other hand, as is essential to quantum mechanical uncertainty, even if the quantum state is known, measurements may still produce an uncertain outcome. In our framework, measurements therefore play the role of acts with an uncertain outcome and our simple decision-theoretic postulates ensure that Born's rule is encapsulated in the utility functions associated with such acts. This approach allows us to uncouple (precise) probability theory from quantum mechanics, in the sense that it leaves room for a more general, so-called imprecise probabilities approach. We discuss the mathematical implications of our findings, which allow us to give a decision-theoretic foundation to recent seminal work by Benavoli, Facchini and Zaffalon, and we compare our approach to earlier and different approaches by Deutsch and Wallace.

Extending choice assessments to choice functions: An algorithm for computing the natural extension

We study how to infer new choices from prior choices using the framework of choice functions, a unifying mathematical framework for decision-making based on sets of preference orders. In particular, we define the natural (most conservative) extension of a given choice assessment to a coherent choice function -- whenever possible -- and use this natural extension to make new choices. We provide a practical algorithm for computing this natural extension and various ways to improve scalability. Finally, we test these algorithms for different types of choice assessments.

A theory of desirable things

Inspired by the theory of desirable gambles that is used to model uncertainty in the field of imprecise probabilities, I present a theory of desirable things. Its aim is to model a subject's beliefs about which things are desirable. What the things are is not important, nor is what it means for them to be desirable. It can be applied to gambles, calling them desirable if a subject accepts them, but it can just as well be applied to pizzas, calling them desirable if my friend Arthur likes to eat them. Other useful examples of things one might apply this theory to are propositions, horse lotteries, or preferences between any of the above. Regardless of the particular things that are considered, inference rules are imposed by means of an abstract closure operator, and models that adhere to these rules are called coherent. I consider two types of models, each of which can capture a subject's beliefs about which things are desirable: sets of desirable things and sets of desirable sets of things. A crucial result is that the latter type can be represented by a set of the former.

The logic behind desirable sets of things, and its filter representation

We identify the logic behind the recent theory of coherent sets of desirable (sets of) things, which generalise desirable (sets of) gambles and coherent choice functions, and show that this identification allows us to establish various representation results for such coherent models in terms of simpler ones.

Decision-making with E-admissibility given a finite assessment of choices

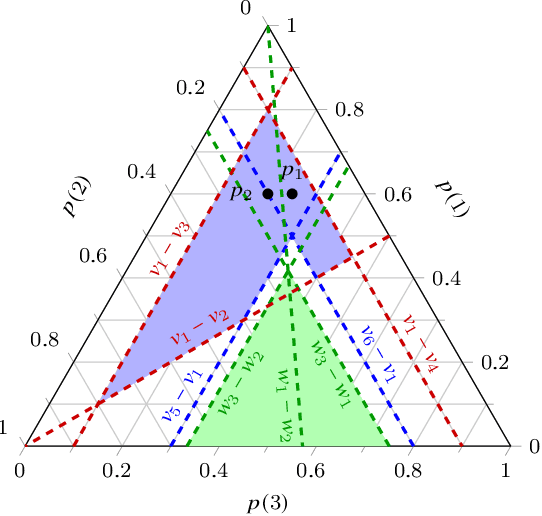
Given information about which options a decision-maker definitely rejects from given finite sets of options, we study the implications for decision-making with E-admissibility. This means that from any finite set of options, we reject those options that no probability mass function compatible with the given information gives the highest expected utility. We use the mathematical framework of choice functions to specify choices and rejections, and specify the available information in the form of conditions on such functions. We characterise the most conservative extension of the given information to a choice function that makes choices based on E-admissibility, and provide an algorithm that computes this extension by solving linear feasibility problems.

On a notion of independence proposed by Teddy Seidenfeld

Teddy Seidenfeld has been arguing for quite a long time that binary preference models are not powerful enough to deal with a number of crucial aspects of imprecision and indeterminacy in uncertain inference and decision making. It is at his insistence that we initiated our study of so-called sets of desirable option sets, which we have argued elsewhere provides an elegant and powerful approach to dealing with general, binary as well as non-binary, decision-making under uncertainty. We use this approach here to explore an interesting notion of irrelevance (and independence), first suggested by Seidenfeld in an example intended as a criticism of a number of specific decision methodologies based on (convex) binary preferences. We show that the consequences of making such an irrelevance or independence assessment are very strong, and might be used to argue for the use of so-called mixing choice functions, and E-admissibility as the resulting decision scheme.

Inference with Choice Functions Made Practical

We study how to infer new choices from previous choices in a conservative manner. To make such inferences, we use the theory of choice functions: a unifying mathematical framework for conservative decision making that allows one to impose axioms directly on the represented decisions. We here adopt the coherence axioms of De Bock and De Cooman (2019). We show how to naturally extend any given choice assessment to such a coherent choice function, whenever possible, and use this natural extension to make new choices. We present a practical algorithm to compute this natural extension and provide several methods that can be used to improve its scalability.

Choice functions based on sets of strict partial orders: an axiomatic characterisation

Methods for choosing from a set of options are often based on a strict partial order on these options, or on a set of such partial orders. I here provide a very general axiomatic characterisation for choice functions of this form. It includes as special cases axiomatic characterisations for choice functions based on (sets of) total orders, (sets of) weak orders, (sets of) coherent lower previsions and (sets of) probability measures.

Archimedean Choice Functions: an Axiomatic Foundation for Imprecise Decision Making

If uncertainty is modelled by a probability measure, decisions are typically made by choosing the option with the highest expected utility. If an imprecise probability model is used instead, this decision rule can be generalised in several ways. We here focus on two such generalisations that apply to sets of probability measures: E-admissibility and maximality. Both of them can be regarded as special instances of so-called choice functions, a very general mathematical framework for decision making. For each of these two decision rules, we provide a set of necessary and sufficient conditions on choice functions that uniquely characterises this rule, thereby providing an axiomatic foundation for imprecise decision making with sets of probabilities. A representation theorem for Archimedean choice functions in terms of coherent lower previsions lies at the basis of both results.