Extending choice assessments to choice functions: An algorithm for computing the natural extension

We study how to infer new choices from prior choices using the framework of choice functions, a unifying mathematical framework for decision-making based on sets of preference orders. In particular, we define the natural (most conservative) extension of a given choice assessment to a coherent choice function -- whenever possible -- and use this natural extension to make new choices. We provide a practical algorithm for computing this natural extension and various ways to improve scalability. Finally, we test these algorithms for different types of choice assessments.

Decision-making with E-admissibility given a finite assessment of choices

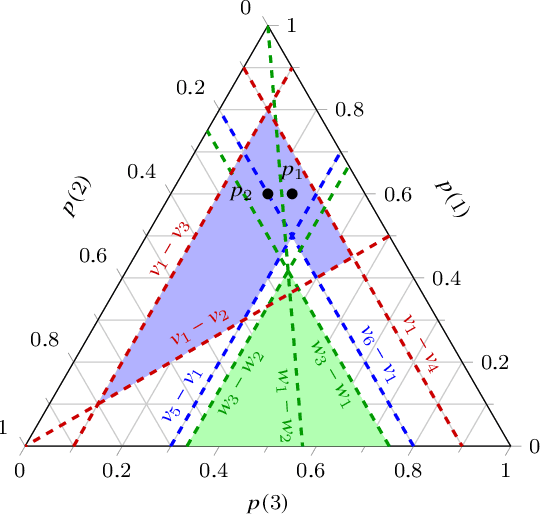
Given information about which options a decision-maker definitely rejects from given finite sets of options, we study the implications for decision-making with E-admissibility. This means that from any finite set of options, we reject those options that no probability mass function compatible with the given information gives the highest expected utility. We use the mathematical framework of choice functions to specify choices and rejections, and specify the available information in the form of conditions on such functions. We characterise the most conservative extension of the given information to a choice function that makes choices based on E-admissibility, and provide an algorithm that computes this extension by solving linear feasibility problems.

Inference with Choice Functions Made Practical

We study how to infer new choices from previous choices in a conservative manner. To make such inferences, we use the theory of choice functions: a unifying mathematical framework for conservative decision making that allows one to impose axioms directly on the represented decisions. We here adopt the coherence axioms of De Bock and De Cooman (2019). We show how to naturally extend any given choice assessment to such a coherent choice function, whenever possible, and use this natural extension to make new choices. We present a practical algorithm to compute this natural extension and provide several methods that can be used to improve its scalability.