Extending choice assessments to choice functions: An algorithm for computing the natural extension

We study how to infer new choices from prior choices using the framework of choice functions, a unifying mathematical framework for decision-making based on sets of preference orders. In particular, we define the natural (most conservative) extension of a given choice assessment to a coherent choice function -- whenever possible -- and use this natural extension to make new choices. We provide a practical algorithm for computing this natural extension and various ways to improve scalability. Finally, we test these algorithms for different types of choice assessments.

Decision-making with E-admissibility given a finite assessment of choices

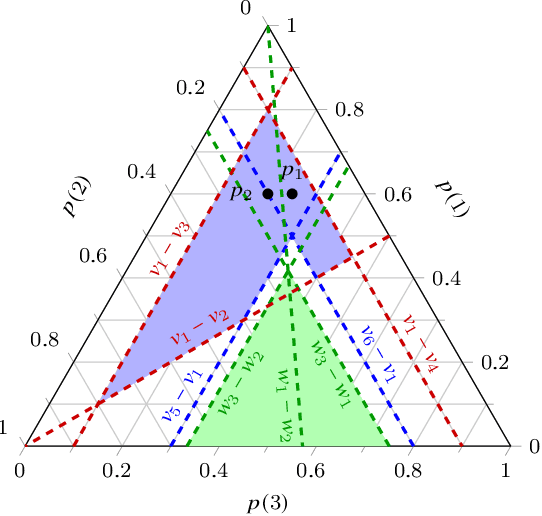
Given information about which options a decision-maker definitely rejects from given finite sets of options, we study the implications for decision-making with E-admissibility. This means that from any finite set of options, we reject those options that no probability mass function compatible with the given information gives the highest expected utility. We use the mathematical framework of choice functions to specify choices and rejections, and specify the available information in the form of conditions on such functions. We characterise the most conservative extension of the given information to a choice function that makes choices based on E-admissibility, and provide an algorithm that computes this extension by solving linear feasibility problems.

An Imprecise Probabilistic Estimator for the Transition Rate Matrix of a Continuous-Time Markov Chain

We consider the problem of estimating the transition rate matrix of a continuous-time Markov chain from a finite-duration realisation of this process. We approach this problem in an imprecise probabilistic framework, using a set of prior distributions on the unknown transition rate matrix. The resulting estimator is a set of transition rate matrices that, for reasons of conjugacy, is easy to find. To determine the hyperparameters for our set of priors, we reconsider the problem in discrete time, where we can use the well-known Imprecise Dirichlet Model. In particular, we show how the limit of the resulting discrete-time estimators is a continuous-time estimator. It corresponds to a specific choice of hyperparameters and has an exceptionally simple closed-form expression.