Machine Learning for Discovering Effective Interaction Kernels between Celestial Bodies from Ephemerides

Building accurate and predictive models of the underlying mechanisms of celestial motion has inspired fundamental developments in theoretical physics. Candidate theories seek to explain observations and predict future positions of planets, stars, and other astronomical bodies as faithfully as possible. We use a data-driven learning approach, extending that developed in Lu et al. ($2019$) and extended in Zhong et al. ($2020$), to a derive stable and accurate model for the motion of celestial bodies in our Solar System. Our model is based on a collective dynamics framework, and is learned from the NASA Jet Propulsion Lab's development ephemerides. By modeling the major astronomical bodies in the Solar System as pairwise interacting agents, our learned model generate extremely accurate dynamics that preserve not only intrinsic geometric properties of the orbits, but also highly sensitive features of the dynamics, such as perihelion precession rates. Our learned model can provide a unified explanation to the observation data, especially in terms of reproducing the perihelion precession of Mars, Mercury, and the Moon. Moreover, Our model outperforms Newton's Law of Universal Gravitation in all cases and performs similarly to, and exceeds on the Moon, the Einstein-Infeld-Hoffman equations derived from Einstein's theory of general relativity.

Learning Interaction Kernels for Agent Systems on Riemannian Manifolds

Interacting agent and particle systems are extensively used to model complex phenomena in science and engineering. We consider the problem of learning interaction kernels in these dynamical systems constrained to evolve on Riemannian manifolds from given trajectory data. The models we consider are based on interaction kernels depending on pairwise Riemannian distances between agents, with agents interacting locally along the direction of the shortest geodesic connecting them. We show that our estimators converge at a rate that is independent of the dimension of the state space, and derive bounds on the trajectory estimation error, on the manifold, between the observed and estimated dynamics. We demonstrate the performance of our estimator on two classical first order interacting systems: Opinion Dynamics and a Predator-Swarm system, with each system constrained on two prototypical manifolds, the $2$-dimensional sphere and the Poincar\'e disk model of hyperbolic space.

Learning Theory for Inferring Interaction Kernels in Second-Order Interacting Agent Systems

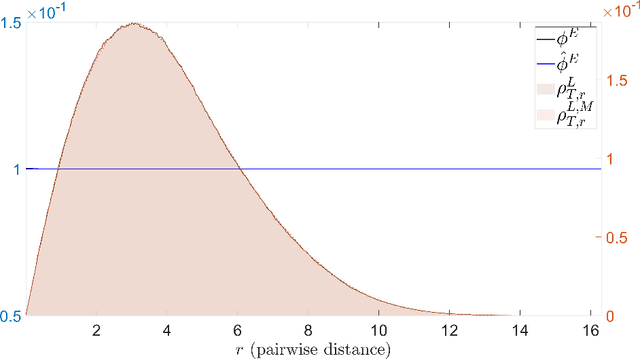
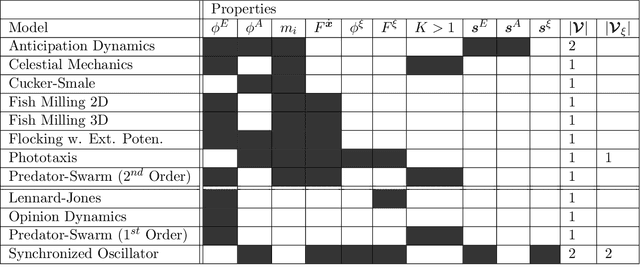
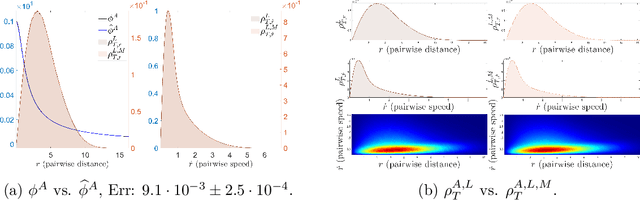
Modeling the complex interactions of systems of particles or agents is a fundamental scientific and mathematical problem that is studied in diverse fields, ranging from physics and biology, to economics and machine learning. In this work, we describe a very general second-order, heterogeneous, multivariable, interacting agent model, with an environment, that encompasses a wide variety of known systems. We describe an inference framework that uses nonparametric regression and approximation theory based techniques to efficiently derive estimators of the interaction kernels which drive these dynamical systems. We develop a complete learning theory which establishes strong consistency and optimal nonparametric min-max rates of convergence for the estimators, as well as provably accurate predicted trajectories. The estimators exploit the structure of the equations in order to overcome the curse of dimensionality and we describe a fundamental coercivity condition on the inverse problem which ensures that the kernels can be learned and relates to the minimal singular value of the learning matrix. The numerical algorithm presented to build the estimators is parallelizable, performs well on high-dimensional problems, and is demonstrated on complex dynamical systems.

Data-driven Discovery of Emergent Behaviors in Collective Dynamics

Particle- and agent-based systems are a ubiquitous modeling tool in many disciplines. We consider the fundamental problem of inferring interaction kernels from observations of agent-based dynamical systems given observations of trajectories, in particular for collective dynamical systems exhibiting emergent behaviors with complicated interaction kernels, in a nonparametric fashion, and for kernels which are parametrized by a single unknown parameter. We extend the estimators introduced in \cite{PNASLU}, which are based on suitably regularized least squares estimators, to these larger classes of systems. We provide extensive numerical evidence that the estimators provide faithful approximations to the interaction kernels, and provide accurate predictions for trajectories started at new initial conditions, both throughout the ``training'' time interval in which the observations were made, and often much beyond. We demonstrate these features on prototypical systems displaying collective behaviors, ranging from opinion dynamics, flocking dynamics, self-propelling particle dynamics, synchronized oscillator dynamics, and a gravitational system. Our experiments also suggest that our estimated systems can display the same emergent behaviors of the observed systems, that occur at larger timescales than those used in the training data. Finally, in the case of families of systems governed by a parameterized family of interaction kernels, we introduce novel estimators that estimate the parameterized family of kernels, splitting it into a common interaction kernel and the action of parameters. We demonstrate this in the case of gravity, by learning both the ``common component'' $1/r^2$ and the dependency on mass, without any a priori knowledge of either one, from observations of planetary motions in our solar system.