Split Conformal Prediction under Data Contamination

Conformal prediction is a non-parametric technique for constructing prediction intervals or sets from arbitrary predictive models under the assumption that the data is exchangeable. It is popular as it comes with theoretical guarantees on the marginal coverage of the prediction sets and the split conformal prediction variant has a very low computational cost compared to model training. We study the robustness of split conformal prediction in a data contamination setting, where we assume a small fraction of the calibration scores are drawn from a different distribution than the bulk. We quantify the impact of the corrupted data on the coverage and efficiency of the constructed sets when evaluated on "clean" test points, and verify our results with numerical experiments. Moreover, we propose an adjustment in the classification setting which we call Contamination Robust Conformal Prediction, and verify the efficacy of our approach using both synthetic and real datasets.

Distribution Free Prediction Sets for Node Classification

Graph Neural Networks (GNNs) are able to achieve high classification accuracy on many large real world datasets, but provide no rigorous notion of predictive uncertainty. We leverage recent advances in conformal prediction to construct prediction sets for node classification in inductive learning scenarios, and verify the efficacy of our approach across standard benchmark datasets using popular GNN models. The code is available at \href{https://github.com/jase-clarkson/graph_cp}{this link}.

Time Series Prediction under Distribution Shift using Differentiable Forgetting

Time series prediction is often complicated by distribution shift which demands adaptive models to accommodate time-varying distributions. We frame time series prediction under distribution shift as a weighted empirical risk minimisation problem. The weighting of previous observations in the empirical risk is determined by a forgetting mechanism which controls the trade-off between the relevancy and effective sample size that is used for the estimation of the predictive model. In contrast to previous work, we propose a gradient-based learning method for the parameters of the forgetting mechanism. This speeds up optimisation and therefore allows more expressive forgetting mechanisms.

DAMNETS: A Deep Autoregressive Model for Generating Markovian Network Time Series

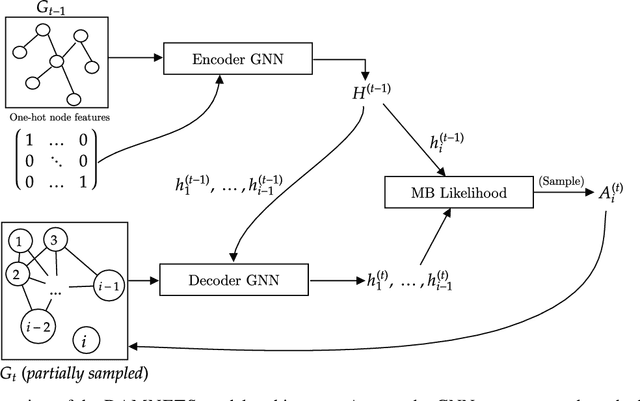
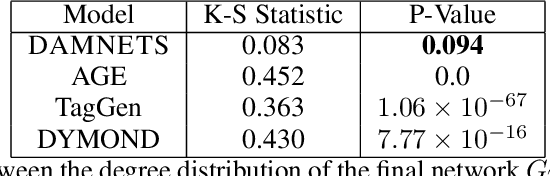
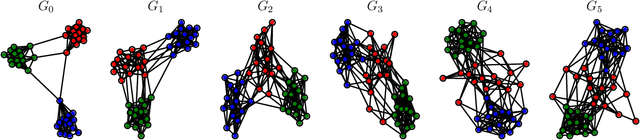
In this work, we introduce DAMNETS, a deep generative model for Markovian network time series. Time series of networks are found in many fields such as trade or payment networks in economics, contact networks in epidemiology or social media posts over time. Generative models of such data are useful for Monte-Carlo estimation and data set expansion, which is of interest for both data privacy and model fitting. Using recent ideas from the Graph Neural Network (GNN) literature, we introduce a novel GNN encoder-decoder structure in which an encoder GNN learns a latent representation of the input graph, and a decoder GNN uses this representation to simulate the network dynamics. We show using synthetic data sets that DAMNETS can replicate features of network topology across time observed in the real world, such as changing community structure and preferential attachment. DAMNETS outperforms competing methods on all of our measures of sample quality over several real and synthetic data sets.