Conformal Prediction for Dose-Response Models with Continuous Treatments

Understanding the dose-response relation between a continuous treatment and the outcome for an individual can greatly drive decision-making, particularly in areas like personalized drug dosing and personalized healthcare interventions. Point estimates are often insufficient in these high-risk environments, highlighting the need for uncertainty quantification to support informed decisions. Conformal prediction, a distribution-free and model-agnostic method for uncertainty quantification, has seen limited application in continuous treatments or dose-response models. To address this gap, we propose a novel methodology that frames the causal dose-response problem as a covariate shift, leveraging weighted conformal prediction. By incorporating propensity estimation, conformal predictive systems, and likelihood ratios, we present a practical solution for generating prediction intervals for dose-response models. Additionally, our method approximates local coverage for every treatment value by applying kernel functions as weights in weighted conformal prediction. Finally, we use a new synthetic benchmark dataset to demonstrate the significance of covariate shift assumptions in achieving robust prediction intervals for dose-response models.

Conformal Monte Carlo Meta-learners for Predictive Inference of Individual Treatment Effects

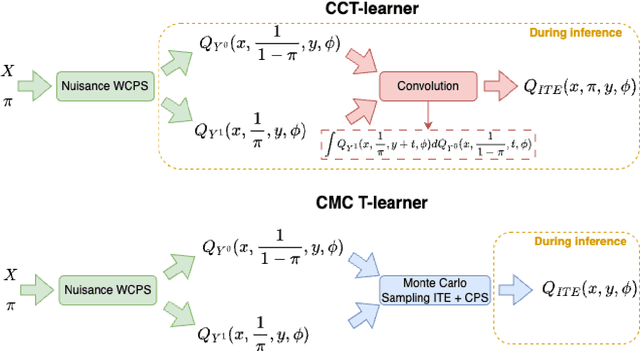
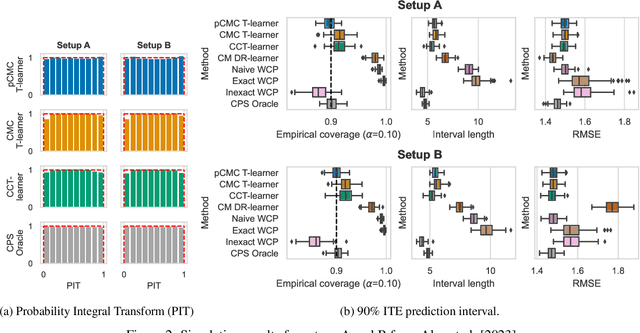
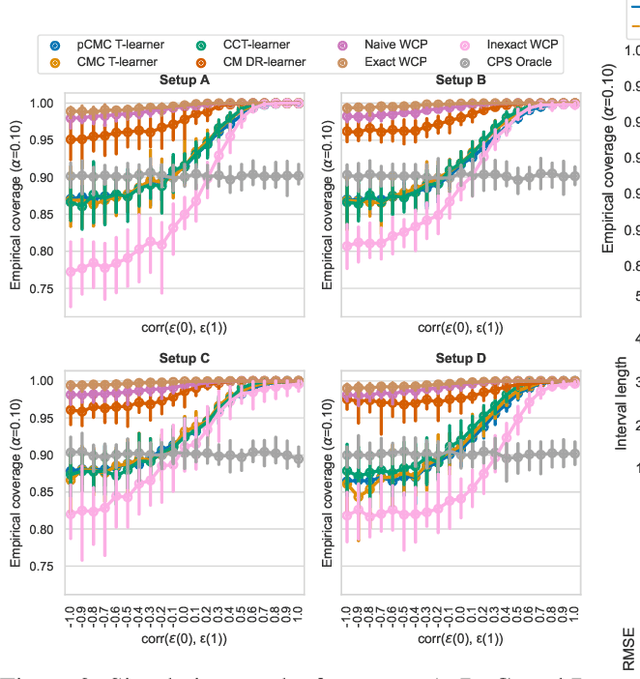
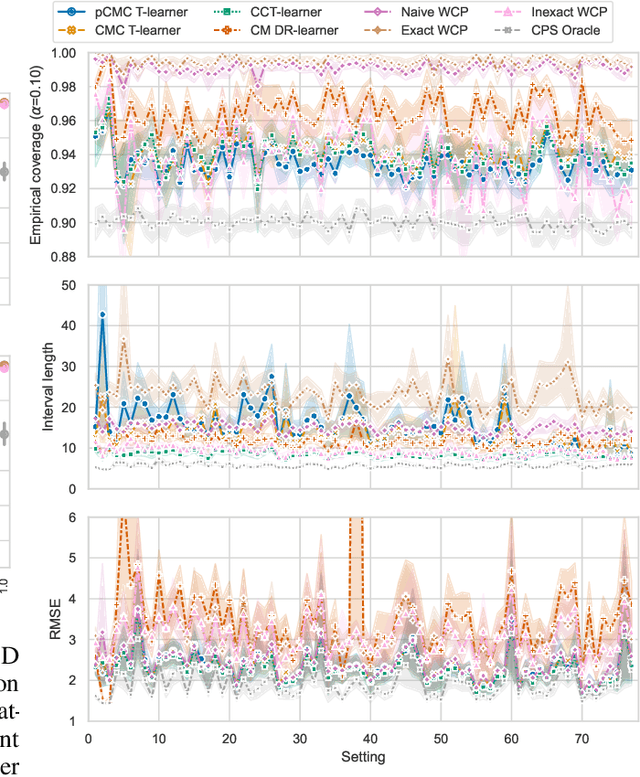
Knowledge of the effect of interventions, called the treatment effect, is paramount for decision-making. Approaches to estimating this treatment effect, e.g. by using Conditional Average Treatment Effect (CATE) estimators, often only provide a point estimate of this treatment effect, while additional uncertainty quantification is frequently desired instead. Therefore, we present a novel method, the Conformal Monte Carlo (CMC) meta-learners, leveraging conformal predictive systems, Monte Carlo sampling, and CATE meta-learners, to instead produce a predictive distribution usable in individualized decision-making. Furthermore, we show how specific assumptions on the noise distribution of the outcome heavily affect these uncertainty predictions. Nonetheless, the CMC framework shows strong experimental coverage while retaining small interval widths to provide estimates of the true individual treatment effect.

Powershap: A Power-full Shapley Feature Selection Method

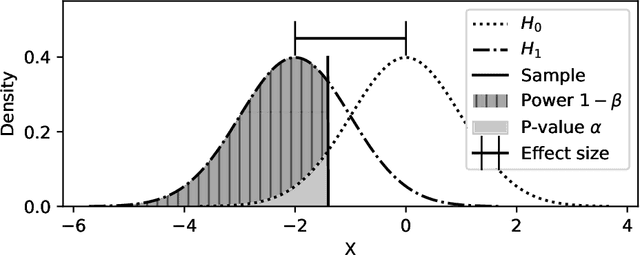
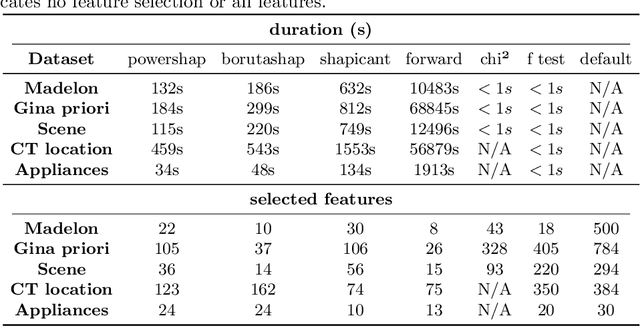
Feature selection is a crucial step in developing robust and powerful machine learning models. Feature selection techniques can be divided into two categories: filter and wrapper methods. While wrapper methods commonly result in strong predictive performances, they suffer from a large computational complexity and therefore take a significant amount of time to complete, especially when dealing with high-dimensional feature sets. Alternatively, filter methods are considerably faster, but suffer from several other disadvantages, such as (i) requiring a threshold value, (ii) not taking into account intercorrelation between features, and (iii) ignoring feature interactions with the model. To this end, we present powershap, a novel wrapper feature selection method, which leverages statistical hypothesis testing and power calculations in combination with Shapley values for quick and intuitive feature selection. Powershap is built on the core assumption that an informative feature will have a larger impact on the prediction compared to a known random feature. Benchmarks and simulations show that powershap outperforms other filter methods with predictive performances on par with wrapper methods while being significantly faster, often even reaching half or a third of the execution time. As such, powershap provides a competitive and quick algorithm that can be used by various models in different domains. Furthermore, powershap is implemented as a plug-and-play and open-source sklearn component, enabling easy integration in conventional data science pipelines. User experience is even further enhanced by also providing an automatic mode that automatically tunes the hyper-parameters of the powershap algorithm, allowing to use the algorithm without any configuration needed.