Reliable uncertainty quantification for 2D/3D anatomical landmark localization using multi-output conformal prediction

Automatic anatomical landmark localization in medical imaging requires not just accurate predictions but reliable uncertainty quantification for effective clinical decision support. Current uncertainty quantification approaches often fall short, particularly when combined with normality assumptions, systematically underestimating total predictive uncertainty. This paper introduces conformal prediction as a framework for reliable uncertainty quantification in anatomical landmark localization, addressing a critical gap in automatic landmark localization. We present two novel approaches guaranteeing finite-sample validity for multi-output prediction: Multi-output Regression-as-Classification Conformal Prediction (M-R2CCP) and its variant Multi-output Regression to Classification Conformal Prediction set to Region (M-R2C2R). Unlike conventional methods that produce axis-aligned hyperrectangular or ellipsoidal regions, our approaches generate flexible, non-convex prediction regions that better capture the underlying uncertainty structure of landmark predictions. Through extensive empirical evaluation across multiple 2D and 3D datasets, we demonstrate that our methods consistently outperform existing multi-output conformal prediction approaches in both validity and efficiency. This work represents a significant advancement in reliable uncertainty estimation for anatomical landmark localization, providing clinicians with trustworthy confidence measures for their diagnoses. While developed for medical imaging, these methods show promise for broader applications in multi-output regression problems.

landmarker: a Toolkit for Anatomical Landmark Localization in 2D/3D Images

Anatomical landmark localization in 2D/3D images is a critical task in medical imaging. Although many general-purpose tools exist for landmark localization in classical computer vision tasks, such as pose estimation, they lack the specialized features and modularity necessary for anatomical landmark localization applications in the medical domain. Therefore, we introduce landmarker, a Python package built on PyTorch. The package provides a comprehensive, flexible toolkit for developing and evaluating landmark localization algorithms, supporting a range of methodologies, including static and adaptive heatmap regression. landmarker enhances the accuracy of landmark identification, streamlines research and development processes, and supports various image formats and preprocessing pipelines. Its modular design allows users to customize and extend the toolkit for specific datasets and applications, accelerating innovation in medical imaging. landmarker addresses a critical need for precision and customization in landmark localization tasks not adequately met by existing general-purpose pose estimation tools.

Conformal Predictive Systems Under Covariate Shift

Conformal Predictive Systems (CPS) offer a versatile framework for constructing predictive distributions, allowing for calibrated inference and informative decision-making. However, their applicability has been limited to scenarios adhering to the Independent and Identically Distributed (IID) model assumption. This paper extends CPS to accommodate scenarios characterized by covariate shifts. We therefore propose Weighted CPS (WCPS), akin to Weighted Conformal Prediction (WCP), leveraging likelihood ratios between training and testing covariate distributions. This extension enables the construction of nonparametric predictive distributions capable of handling covariate shifts. We present theoretical underpinnings and conjectures regarding the validity and efficacy of WCPS and demonstrate its utility through empirical evaluations on both synthetic and real-world datasets. Our simulation experiments indicate that WCPS are probabilistically calibrated under covariate shift.

Conformal Monte Carlo Meta-learners for Predictive Inference of Individual Treatment Effects

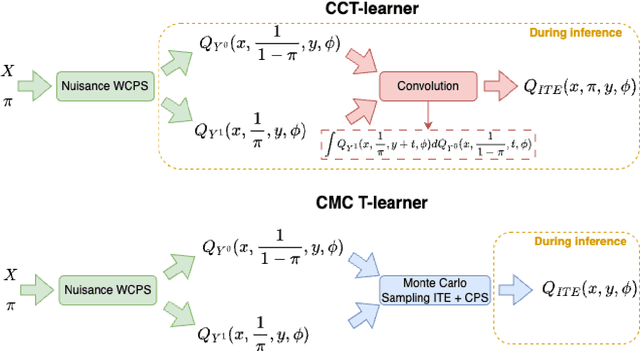
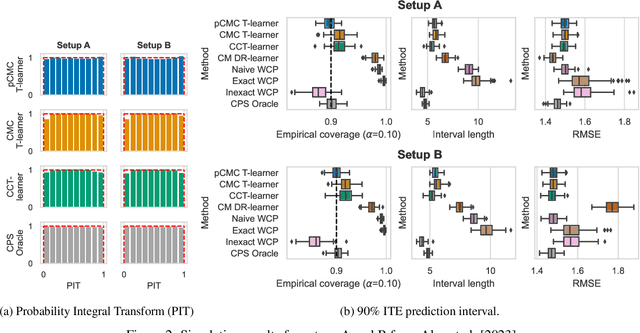
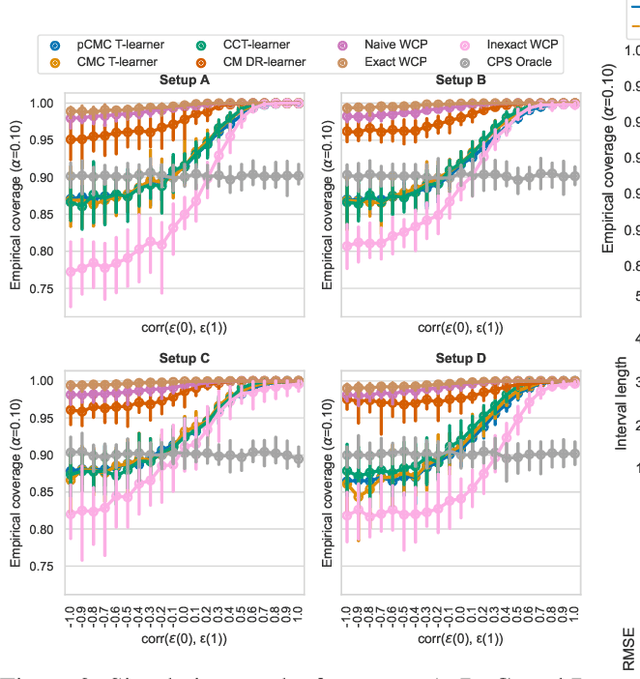
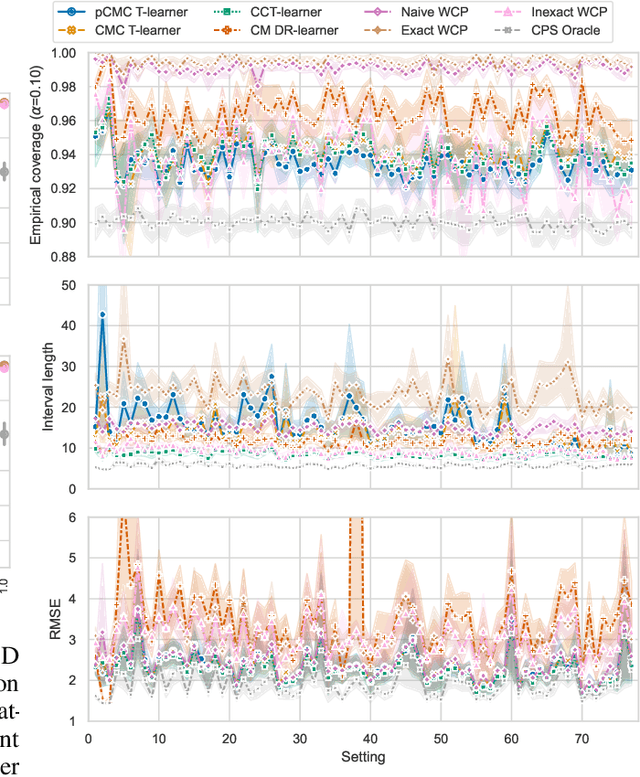
Knowledge of the effect of interventions, called the treatment effect, is paramount for decision-making. Approaches to estimating this treatment effect, e.g. by using Conditional Average Treatment Effect (CATE) estimators, often only provide a point estimate of this treatment effect, while additional uncertainty quantification is frequently desired instead. Therefore, we present a novel method, the Conformal Monte Carlo (CMC) meta-learners, leveraging conformal predictive systems, Monte Carlo sampling, and CATE meta-learners, to instead produce a predictive distribution usable in individualized decision-making. Furthermore, we show how specific assumptions on the noise distribution of the outcome heavily affect these uncertainty predictions. Nonetheless, the CMC framework shows strong experimental coverage while retaining small interval widths to provide estimates of the true individual treatment effect.