Conformal Monte Carlo Meta-learners for Predictive Inference of Individual Treatment Effects
Paper and Code
Feb 07, 2024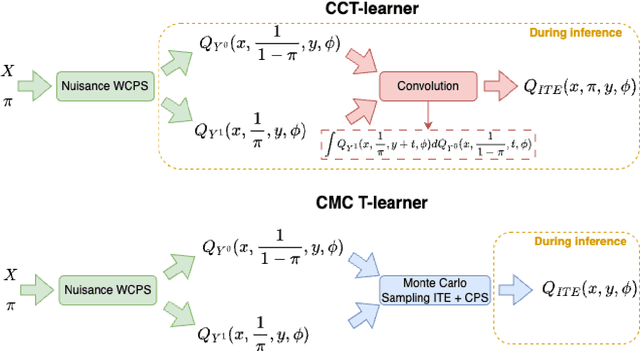
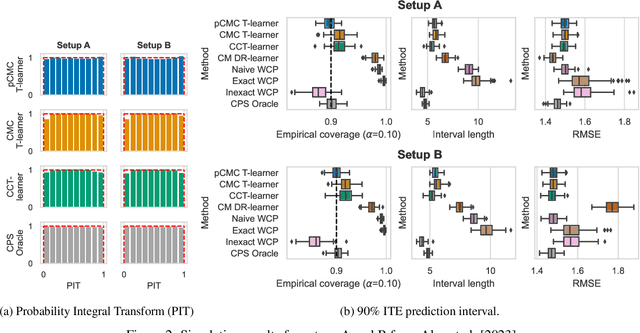
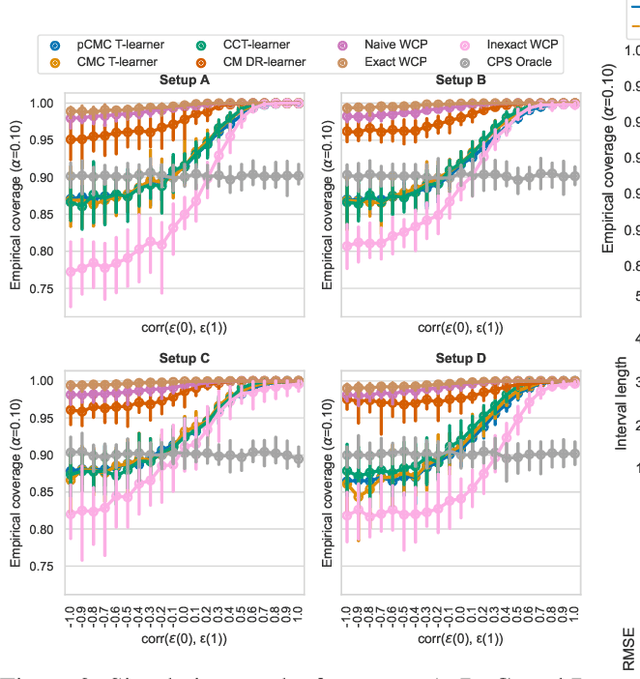
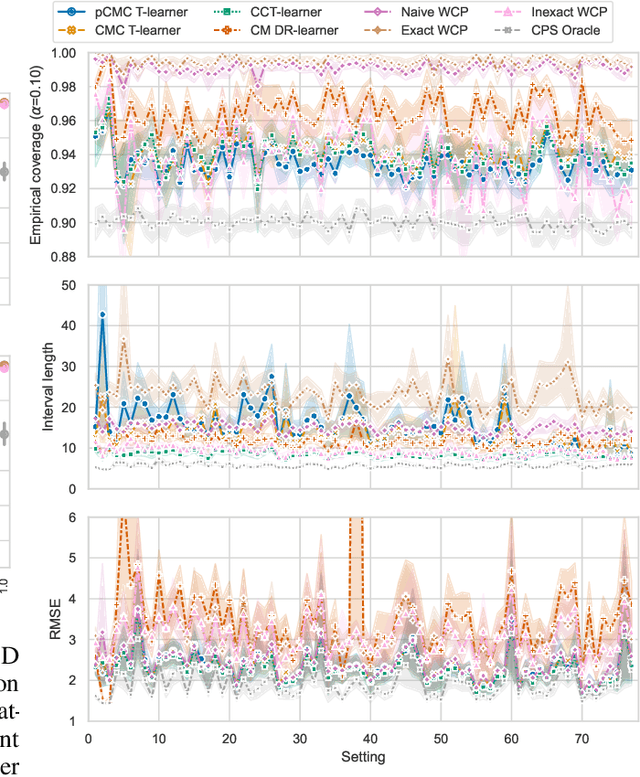
Knowledge of the effect of interventions, called the treatment effect, is paramount for decision-making. Approaches to estimating this treatment effect, e.g. by using Conditional Average Treatment Effect (CATE) estimators, often only provide a point estimate of this treatment effect, while additional uncertainty quantification is frequently desired instead. Therefore, we present a novel method, the Conformal Monte Carlo (CMC) meta-learners, leveraging conformal predictive systems, Monte Carlo sampling, and CATE meta-learners, to instead produce a predictive distribution usable in individualized decision-making. Furthermore, we show how specific assumptions on the noise distribution of the outcome heavily affect these uncertainty predictions. Nonetheless, the CMC framework shows strong experimental coverage while retaining small interval widths to provide estimates of the true individual treatment effect.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge