Meta-analysis of individualized treatment rules via sign-coherency

Medical treatments tailored to a patient's baseline characteristics hold the potential of improving patient outcomes while reducing negative side effects. Learning individualized treatment rules (ITRs) often requires aggregation of multiple datasets(sites); however, current ITR methodology does not take between-site heterogeneity into account, which can hurt model generalizability when deploying back to each site. To address this problem, we develop a method for individual-level meta-analysis of ITRs, which jointly learns site-specific ITRs while borrowing information about feature sign-coherency via a scientifically-motivated directionality principle. We also develop an adaptive procedure for model tuning, using information criteria tailored to the ITR learning problem. We study the proposed methods through numerical experiments to understand their performance under different levels of between-site heterogeneity and apply the methodology to estimate ITRs in a large multi-center database of electronic health records. This work extends several popular methodologies for estimating ITRs (A-learning, weighted learning) to the multiple-sites setting.

A Methodological Framework for the Comparative Evaluation of Multiple Imputation Methods: Multiple Imputation of Race, Ethnicity and Body Mass Index in the U.S. National COVID Cohort Collaborative

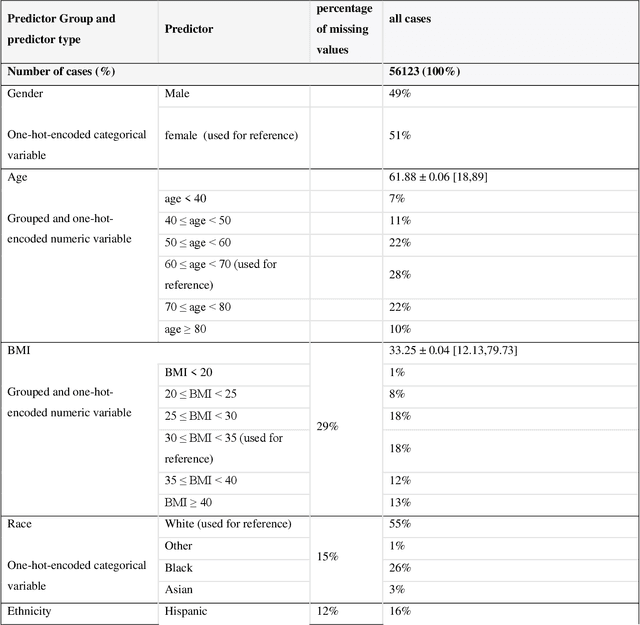
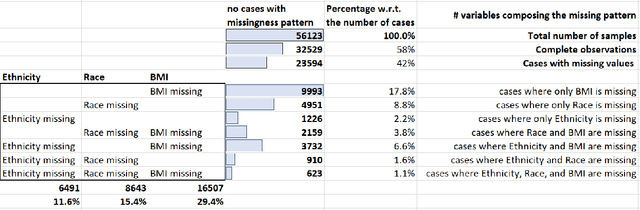
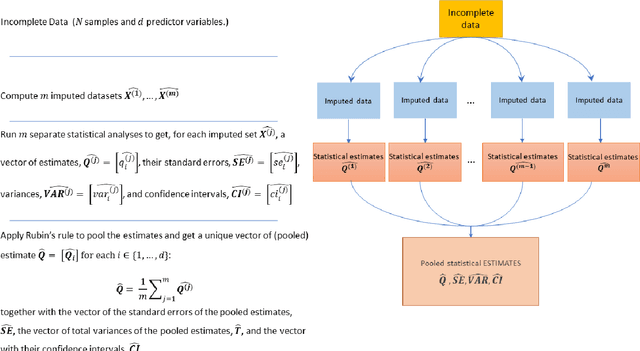
While electronic health records are a rich data source for biomedical research, these systems are not implemented uniformly across healthcare settings and significant data may be missing due to healthcare fragmentation and lack of interoperability between siloed electronic health records. Considering that the deletion of cases with missing data may introduce severe bias in the subsequent analysis, several authors prefer applying a multiple imputation strategy to recover the missing information. Unfortunately, although several literature works have documented promising results by using any of the different multiple imputation algorithms that are now freely available for research, there is no consensus on which MI algorithm works best. Beside the choice of the MI strategy, the choice of the imputation algorithm and its application settings are also both crucial and challenging. In this paper, inspired by the seminal works of Rubin and van Buuren, we propose a methodological framework that may be applied to evaluate and compare several multiple imputation techniques, with the aim to choose the most valid for computing inferences in a clinical research work. Our framework has been applied to validate, and extend on a larger cohort, the results we presented in a previous literature study, where we evaluated the influence of crucial patients' descriptors and COVID-19 severity in patients with type 2 diabetes mellitus whose data is provided by the National COVID Cohort Collaborative Enclave.

Robust Sample Weighting to Facilitate Individualized Treatment Rule Learning for a Target Population

Learning individualized treatment rules (ITRs) is an important topic in precision medicine. Current literature mainly focuses on deriving ITRs from a single source population. We consider the observational data setting when the source population differs from a target population of interest. We assume subject covariates are available from both populations, but treatment and outcome data are only available from the source population. Although adjusting for differences between source and target populations can potentially lead to an improved ITR for the target population, it can substantially increase the variability in ITR estimation. To address this dilemma, we develop a weighting framework that aims to tailor an ITR for a given target population and protect against high variability due to superfluous covariate shift adjustments. Our method seeks covariate balance over a nonparametric function class characterized by a reproducing kernel Hilbert space and can improve many ITR learning methods that rely on weights. We show that the proposed method encompasses importance weights and the so-called overlap weights as two extreme cases, allowing for a better bias-variance trade-off in between. Numerical examples demonstrate that the use of our weighting method can greatly improve ITR estimation for the target population compared with other weighting methods.