WaveGAS: Waveform Relaxation for Scaling Graph Neural Networks

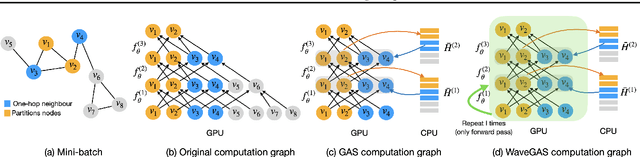
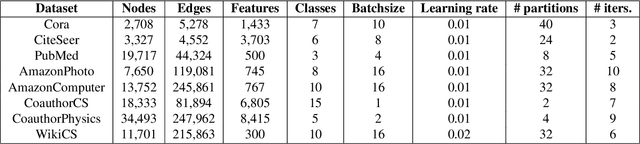
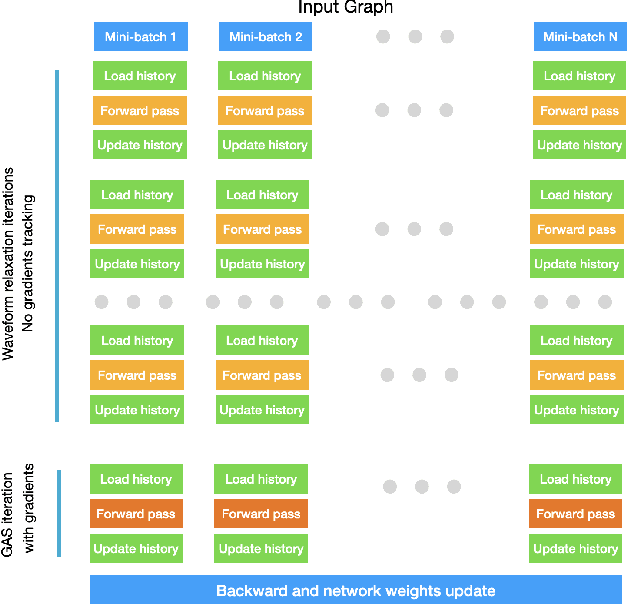
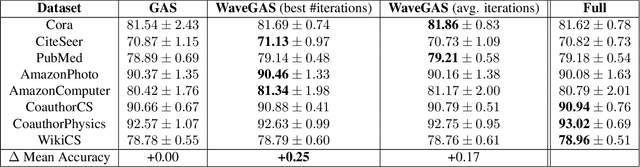
With the ever-growing size of real-world graphs, numerous techniques to overcome resource limitations when training Graph Neural Networks (GNNs) have been developed. One such approach, GNNAutoScale (GAS), uses graph partitioning to enable training under constrained GPU memory. GAS also stores historical embedding vectors, which are retrieved from one-hop neighbors in other partitions, ensuring critical information is captured across partition boundaries. The historical embeddings which come from the previous training iteration are stale compared to the GAS estimated embeddings, resulting in approximation errors of the training algorithm. Furthermore, these errors accumulate over multiple layers, leading to suboptimal node embeddings. To address this shortcoming, we propose two enhancements: first, WaveGAS, inspired by waveform relaxation, performs multiple forward passes within GAS before the backward pass, refining the approximation of historical embeddings and gradients to improve accuracy; second, a gradient-tracking method that stores and utilizes more accurate historical gradients during training. Empirical results show that WaveGAS enhances GAS and achieves better accuracy, even outperforming methods that train on full graphs, thanks to its robust estimation of node embeddings.

Vision Paper: Designing Graph Neural Networks in Compliance with the European Artificial Intelligence Act

The European Union's Artificial Intelligence Act (AI Act) introduces comprehensive guidelines for the development and oversight of Artificial Intelligence (AI) and Machine Learning (ML) systems, with significant implications for Graph Neural Networks (GNNs). This paper addresses the unique challenges posed by the AI Act for GNNs, which operate on complex graph-structured data. The legislation's requirements for data management, data governance, robustness, human oversight, and privacy necessitate tailored strategies for GNNs. Our study explores the impact of these requirements on GNN training and proposes methods to ensure compliance. We provide an in-depth analysis of bias, robustness, explainability, and privacy in the context of GNNs, highlighting the need for fair sampling strategies and effective interpretability techniques. Our contributions fill the research gap by offering specific guidance for GNNs under the new legislative framework and identifying open questions and future research directions.

Choosing a Classical Planner with Graph Neural Networks

Online planner selection is the task of choosing a solver out of a predefined set for a given planning problem. As planning is computationally hard, the performance of solvers varies greatly on planning problems. Thus, the ability to predict their performance on a given problem is of great importance. While a variety of learning methods have been employed, for classical cost-optimal planning the prevailing approach uses Graph Neural Networks (GNNs). In this work, we continue the line of work on using GNNs for online planner selection. We perform a thorough investigation of the impact of the chosen GNN model, graph representation and node features, as well as prediction task. Going further, we propose using the graph representation obtained by a GNN as an input to the Extreme Gradient Boosting (XGBoost) model, resulting in a more resource-efficient yet accurate approach. We show the effectiveness of a variety of GNN-based online planner selection methods, opening up new exciting avenues for research on online planner selection.

The Evolution of Distributed Systems for Graph Neural Networks and their Origin in Graph Processing and Deep Learning: A Survey

Graph Neural Networks (GNNs) are an emerging research field. This specialized Deep Neural Network (DNN) architecture is capable of processing graph structured data and bridges the gap between graph processing and Deep Learning (DL). As graphs are everywhere, GNNs can be applied to various domains including recommendation systems, computer vision, natural language processing, biology and chemistry. With the rapid growing size of real world graphs, the need for efficient and scalable GNN training solutions has come. Consequently, many works proposing GNN systems have emerged throughout the past few years. However, there is an acute lack of overview, categorization and comparison of such systems. We aim to fill this gap by summarizing and categorizing important methods and techniques for large-scale GNN solutions. In addition, we establish connections between GNN systems, graph processing systems and DL systems.